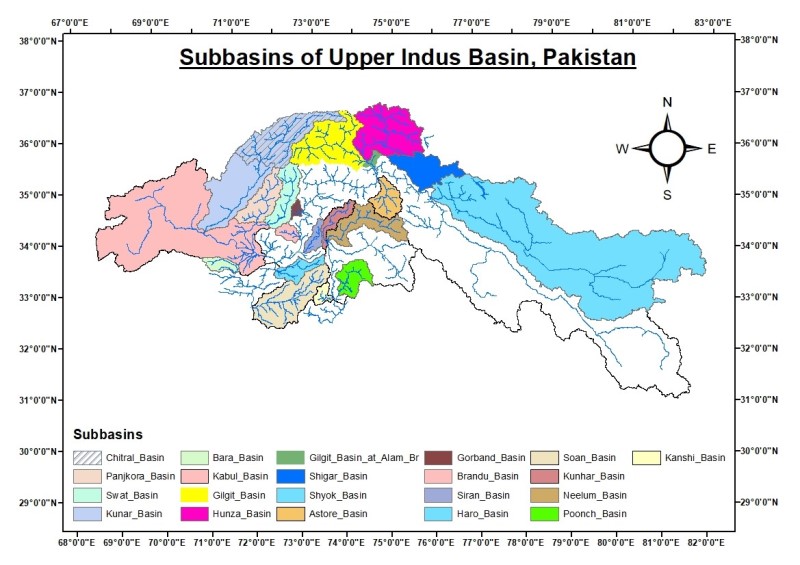
This section provides an overview of the findings and analyses related to features including stream order, stream length, mean stream length, stream length ratio, bifurcation ratio, length of overland flow, basin length, and perimeter, constitutes the morphometric examination of a basin.

The comprehension of stream order and stream numbers is of great significance within the discipline of fluvial geomorphology. The drainage network is of paramount importance in facilitating the conveyance of water and sediments from a specific basin via a solitary outlet. The greatest rank of the basin is attributed to this distinctive outlet, therefore signifying its classification as the basin's order. The dimensions of rivers and basins exhibit significant variety by the hierarchical structure of the basin. The first step in basin analysis involves the arrangement and structure of stream networks. To conduct a thorough examination of basin characteristics, it is essential to undertake a rigorous investigation of the many aspects associated with stream networks [18]. 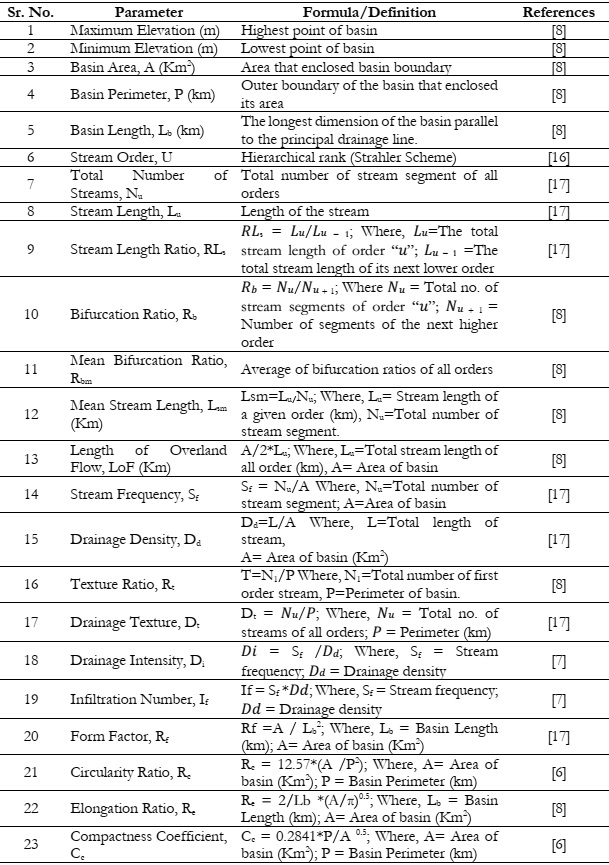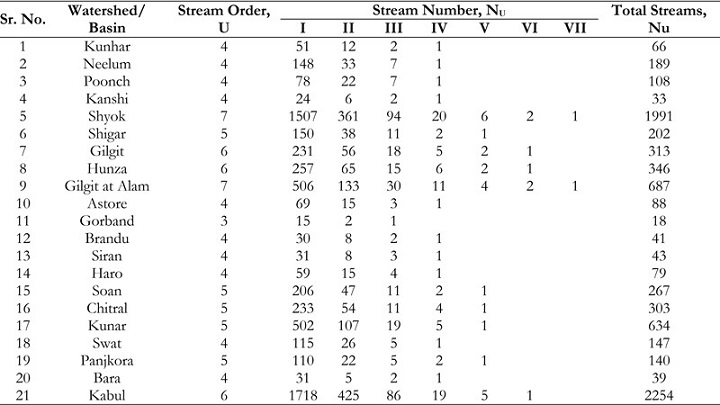This study has conducted a stream rating assessment using the suggested methodologies. The assessment of stream order was carried out in a comprehensive set of 21 subbasins, wherein the observed stream orders exhibited a range spanning from 3 to 7. The subbasins where the highest stream order, specifically defined as 7, is seen encompass the Shyok River and the Gilgit River basin. This phenomenon occurs near the confluence where the Indus River crosses with the Alam Bridge. In contrast, the Gorband basin exhibits the minimum stream order, which is designated as 3. Table 2 presents the quantitative data about the streams linked to each stream order within the 21 subbasins of the Indus basin. Although most basins have a drainage pattern of the fourth order, the five studied basins had streams of the fifth order. The streams located in the Hunza, Gilgit, and Kabul basins demonstrated a classification of the 6th order. The prevailing drainage patterns observed in all basins of the stream network are commonly described as sub-dendritic to dendritic. The observation noted above suggests that there is a uniform texture and a lack of structural influence, as depicted in Figure 2. The prevalence of first-order streams is observed to be the highest among all stream orders. Furthermore, Figure 3 (See at the end of Paper) illustrates a decrease in the overall number of stream segments as the stream order increases. The discovery cited above suggests that the entire region has a consistent lithological composition. Furthermore, from a geological perspective, there are no observable signs of uplift occurring inside the basin. The Kabul basin exhibits the highest number of streams, totaling 2,254.

The measurement of stream Length has been carried out utilizing the methodologies proposed by Horton, which is a significant hydrological metric in a basin since it offers useful insights on the characteristics of surface runoff. Watersheds characterized by effective drainage often demonstrate the presence of permeable bedrock and formations, as seen by a scarcity of elongated streams. Conversely, watersheds characterized by bedrock and formations with limited permeability display a higher prevalence of shorter streams. This claim is substantiated by prior scholarly investigations. Typically, stream segments demonstrate a higher overall length in streams of first order, followed by a drop in length as stream order increases. The research entailed the quantification of stream networks of varying orders within a certain watershed, together with the computation of their respective lengths from the discharge point to the point of drainage split. The accomplishment was achieved by the application of GIS software. Table 3 presents the findings about the lengths of streams in each of the 21 subbasins, arranged sequentially. The data depicted in Figure 2 provides compelling and incontrovertible evidence of a positive association between stream order and cumulative stream length. A positive link has been observed between stream order and the characteristics displayed by first-order streams. As the order of a stream increases, there is a tendency for these values to gradually decrease [19]. The Shyok basin displayed a notable discrepancy in the lengths of its streams of different orders, specifically between the first-order and seventh-order streams. The former had a remarkable span of 8400 km, and the latter possessed a relatively shorter extent of 320 km. The Kabul basin demonstrated the highest aggregate stream length, reaching a total of 17,528 km.

Table 2: Stream order and stream number of mountainous watersheds of UIB, Pakistan.

The Mean Stream Length (SLm) is an essential attribute that is linked to the drainage network and the landforms it contains (15). The SLm values for all 21 subbasins demonstrate a range of 3.76 to 365.73 km, with variances seen within various stream orders. The Soan basin exhibits the most elevated SLm, at 9.49 km. Table 4 presents a comprehensive comparative analysis of the Land Surface Models (LSMs) about each subbasin. A positive association has been shown between stream order and the average length of streams, suggesting that a rise in stream order is associated with a corresponding increase in the average length of streams. Previous studies have noted that the SLm value of a stream order consistently displays a greater magnitude in comparison to that of a lower order. Conversely, the SLm value of a lower order consistently exhibits a smaller magnitude when compared to that of a higher order. The variety observed in the SLm values across various subbasins can be attributed to their close correlation with the size and terrain of these subbasins [20].

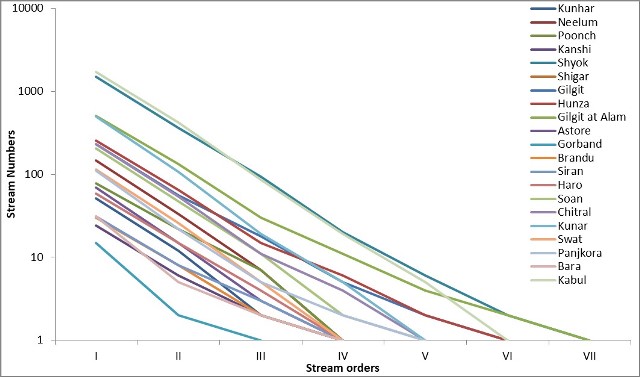
Figure 2: Relationship between stream order and number of streams for 21 sub-watersheds.

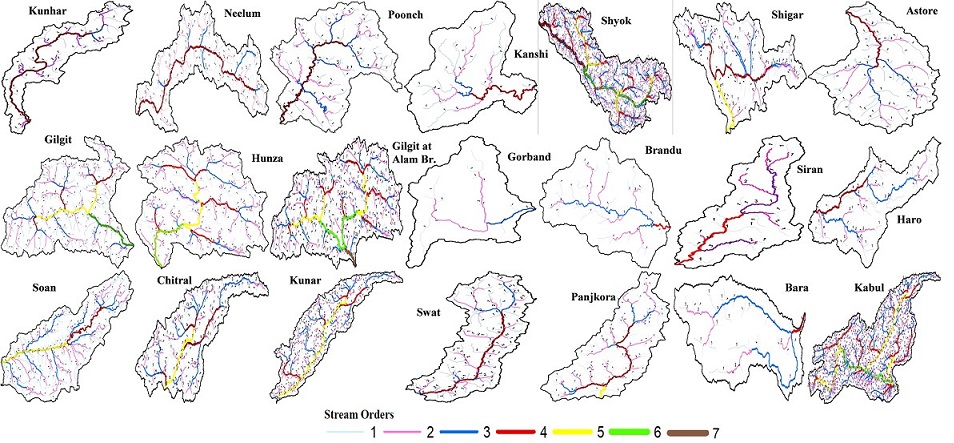
Figure 3: Stream order of sub-watersheds of UIB, Pakistan.

Table 3: Stream lengths of mountainous watersheds of UIB, Pakistan.

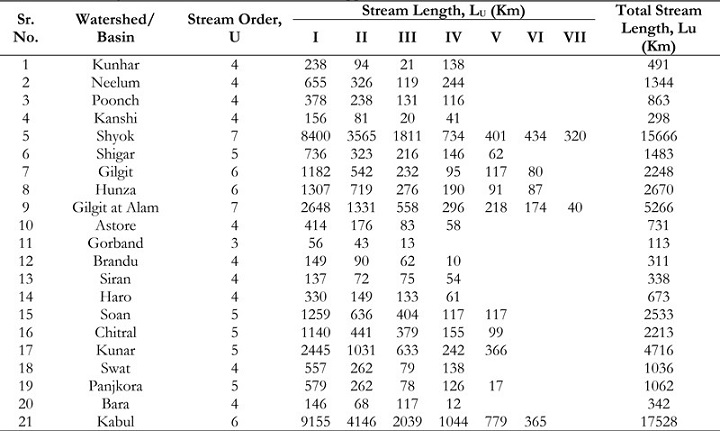
Table 4: SLm of mountainous watersheds of UIB, Pakistan.

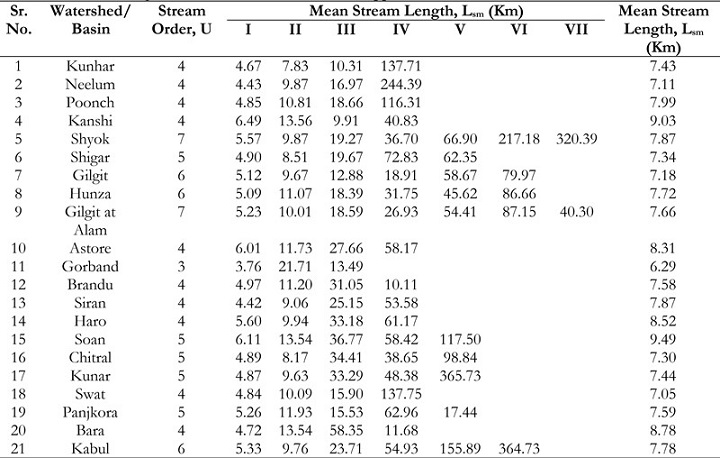
The Stream Length Ratio (SLR) is a statistical measure used to objectively evaluate the relationship between the lengths of different streams. The SLR values are displayed in Table 5. The variability in stream lengths across streams of varying orders within each subbasin is observed within each specific subwatershed. The observed alteration can be ascribed to fluctuations in the incline and topography, suggesting that the streams are presently in a phase of advanced youth with regards to geomorphic evolution [21].

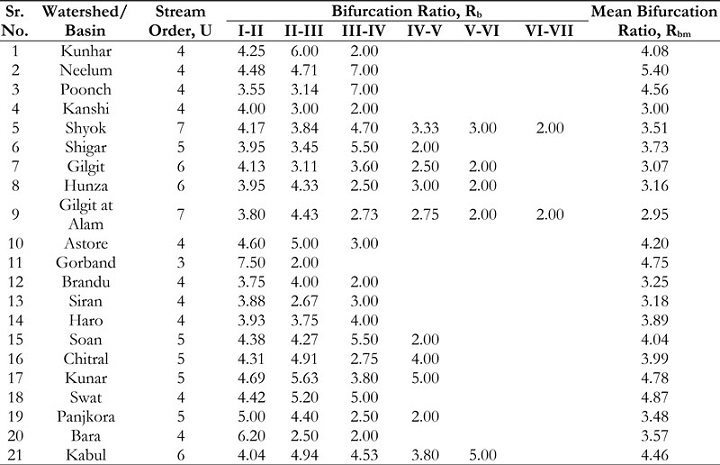
The Bifurcation Ratio, denoted as BR, is a quantitative measure utilized in several academic disciplines to assess the branching pattern of a certain system. The dimensionless quantity under consideration functions as a measure of the level of connectivity between streams of different orders within a certain drainage basin. The data reported in Table 6 demonstrates that the Rb values observed in all 21 subbasins display a variation ranging from 2.00 to 6.20. The Mean Bifurcation Ratio (MBR) displays a spectrum of values ranging from 3.00 to 5.40. The Neelum watershed demonstrates the highest values of MBR, specifically 5.40, indicating an early peak in the hydrograph and a reduced lag time within the basin. The aforementioned observation suggests that the structural variables have a substantial impact on the establishment of drainage patterns within this watershed. The regions of Kanshi and Shigar exhibit the lowest MBR levels, specifically at 3.0 and 3.07, respectively. The aforementioned numerical values suggest a delayed occurrence of the peak in the hydrograph. Based on the research conducted by Strahler in 1964, it was observed that the bifurcation ratio often falls within the range of 3.0 to 5.0 in drainage basins that have not undergone any geological alterations [22]. All subbasins encompassed within this range exhibit geologically favorable formations that do not exert any discernible impact on the drainage pattern. The provided MBR values presented in Table 6 illustrate an immediate peak observed in the hydrograph, indicating a relatively shorter lag period for the basin.

Table 5: Stream length ratios of mountainous watersheds of UIB, Pakistan

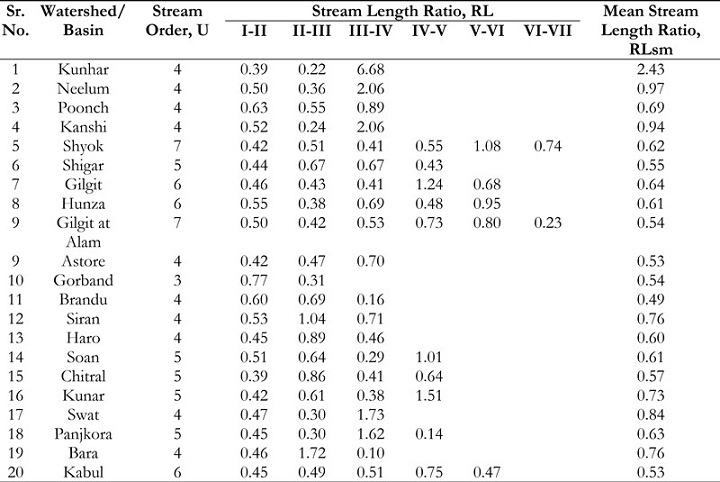
Table 6: BR of mountainous watersheds of UIB, Pakistan.

The determination of the perimeter of a basin, denoted as P, is achieved through the measurement of the cumulative length along the boundaries that delineate separate watersheds. The aforementioned metric possesses the capacity to serve as an evaluative tool for analyzing the many aspects and structures of a particular watershed. The various perimeters of the subbasins within the UIB are presented in Table 7, ranging from 180 km to 3138 km. The Kabul basin exhibits the largest diameter, measuring 3138 km in length [23].

The Length of Overland Flow (LOF) refers to the distance that water travels across the land surface before it converges into a well-defined stream channel. The Landform variable, often known as LOF, plays a significant role in shaping the hydrologic and physiographic characteristics of drainage basins. The estimation of length of overland flow can be estimated as approximately 0.5 times the inverse of DD [24]. The aforementioned element demonstrates a negative link with the average gradient of the channel and displays a significant association with the magnitude of sheet flow. The research domain exhibits a range of LOF values, varying from 2.16 to 2.95 km, as illustrated in Table 7.

Table 7: Area, perimeter, longest flow path, and length of overland flow of mountainous watersheds of UIB, Pakistan.

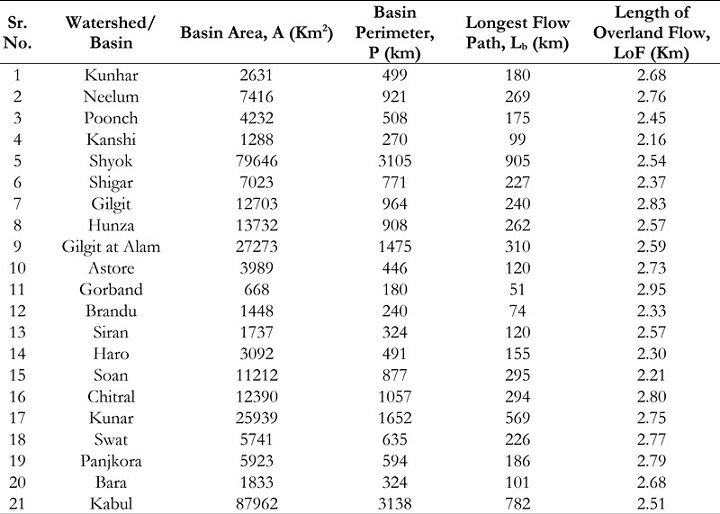
Table 7 illustrates the considerable disparity in the Longest Flow Path (LFP) among the subbasins of the UIB, with a range of values spanning from 51 km to 905 km. The Shyok basin exhibits a considerable perimeter, measuring 905 km [25].

Key Attributes of Aerial Phenomena:

The morphometric analysis of a basin revealed that a positive correlation has been seen between the size of a watershed and the rates of runoff volume [26]. The evaluation of the maximum rate at which runoff occurs holds substantial significance in the development of erosion control structures and channels designed to accept the highest possible volume of runoff. The drainage areas of the subbasins within UIB exhibit significant variation, with values ranging from 668 km2 to 87,962 km2, as documented in Table 7. The Kabul basin exhibits a substantial extent in terms of its geographical dimensions. All 21 subbasins have been classified into four distinct groups based on their respective sizes. The classification of these groups is as follows: the watershed group, which contains areas up to 1,000 km2; the sub-catchment group, which ranges from 1,000 to 7,000 km2; the catchment group, spanning from 7,000 to 30,000 km2; and the basin group, which includes territories between 30,000 and 95,000 km2. Based on the aforementioned criteria, it is apparent that two basins have been identified within the watershed, whilst ten basins have been classified as sub-catchments. Moreover, a comprehensive analysis has revealed a total of eight basins as catchments, with two basins being explicitly designated as basins, as depicted in Figure 4. The Shyok and Kabul River basins are situated within the encompassing basin [27].

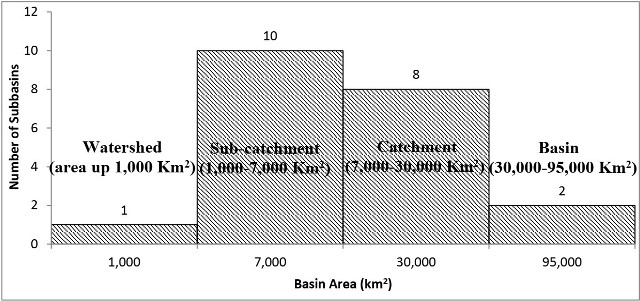
Figure 4: Number of basins by drainage basin area.

The concept of DD pertains to the proximity of channel spacing and serves as a quantitative measure of landscape fragmentation and the probability of surface runoff. The density factor is subject to the influence of multiple factors, such as climate, rock composition, topography, infiltration capacity, vegetation density, and run-off intensity index. The computed values of DD within the UIB region is shown in Table 8, which demonstrates a variation ranging from 0.170 to 0.231 km-1. The numbers given above are indicative of the presence of regions characterized by the existence of resilient permeable material, abundant vegetation, and minimal topographic variation. Consequently, these areas exhibit a greater propensity for infiltration and might be considered favorable sites for groundwater recharge when compared to watersheds characterized by high DD values. Based on the variable DD, it can be inferred that Gilgit will exhibit the longest basin lag time, while Soan will have the smallest lag time [28]. A positive association has been observed between the Frequency of Streams (FS) and the DD within the watershed. This suggested that an increase in DD is associated with a greater number of streams. The recorded values of Fs in each subbasin are displayed in Table 8, exhibiting a range spanning from 0.021 to 0.029. The data demonstrated suggests a noteworthy occurrence of markedly low Fs values. The analysis of stream frequency data revealed a very sparse distribution of streams inside the subbasins. Furthermore, this observation implied that the basin exhibits a restricted quantity of drainage outlets or conduits. The rationale behind this phenomenon can be attributed to the sedimentary geology of the particular study site. This suggested that there are constraints on the availability of storm runoff, which could potentially lead to the occurrence of a devastating flood event. The probability of flooding escalates when the capacity of a limited number of water outlets is rapidly surpassed, both during and following a storm event. The importance of the Texture Ratio (TR) in evaluating drainage morphometrics has been highlighted. The significance of Drainage Texture (DT) is highly relevant in the field of geomorphology as it pertains to the spatial organization of drainage lines. The attributes of drainage are subject to the effect of lithology, infiltration capacity, and topographic characteristics of the terrain. This study presents a taxonomy for characterizing DT, which encompasses five distinct classifications: very coarse (less than 2), coarse (2 to 4), moderate (4 to 6), fine (6 to 8), and very fine (more than 8). The findings of the study are presented in Table 8, indicating that the values for all basins are below 2. This suggested that the drainage texture of these basins can be classified as very coarse [18]. The concept of Drainage Intensity (DI) suggests that when the DI value is low, the impact of DD and stream frequency on the degree of surface erosion caused by denudation agents is minimal or negligible. The findings shown in Table 8 demonstrate a correlation between the values of DI and a decrease in DD, stream frequency, and drainage intensity. These factors, when combined, work together to result in a reduced rate of surface runoff removal within the watershed. Consequently, this particular situation renders the watershed more vulnerable to the incidence of flooding, gully erosion, and landslides [13].

Table 8: SF, DD, TR, DT, DI, and IN of Mountain Watersheds in Pakistan's UIB.

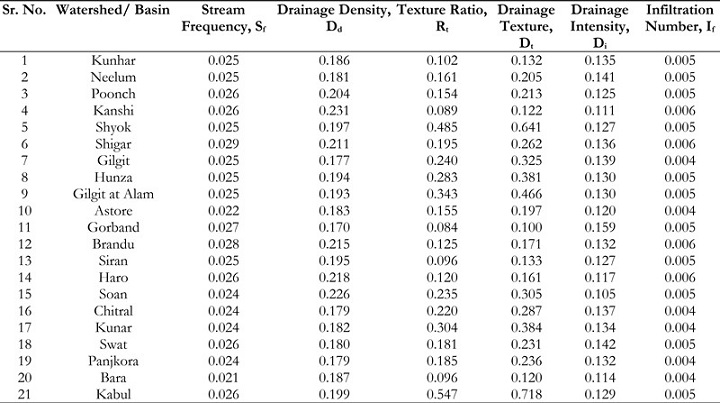
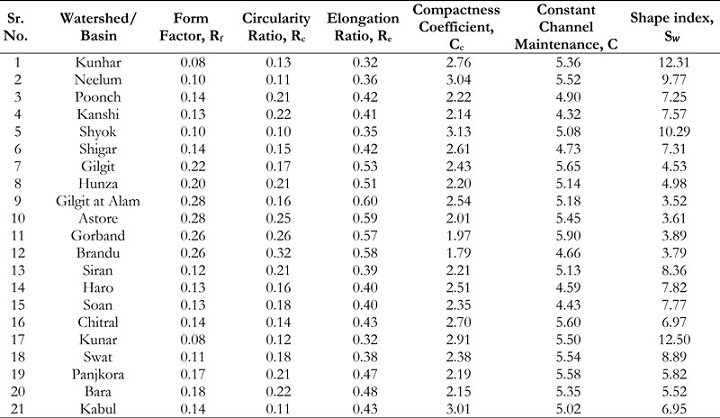
The Infiltration Number (IN) is seen to vary within the range of 0.004 and 0.006, as reported in Table 8 of the current research. Within the specific environment being considered, the presence of low values may indicate a heightened level of infiltration and a diminished level of run-off. The present analysis provides significant insights into the infiltration features of the watershed. The Form Factor (FF) is a numerical metric that regularly exhibits values below 0.754, indicating the existence of a watershed with a perfectly circular morphology. Basins characterized by high FF are correlated with elevated peak flows of relatively shorter periods, while extended subwatersheds with low form factors exhibit reduced peak flow rates that persist for longer durations. The FF values for each of the 21 subbasins are displayed in Table 8. These values indicate elongated shapes and imply the existence of prolonged periods with flat hydrograph peaks.

The Circularity Ratio (CR) has been shown in Table 8 which displays the range of Rc values for various sub-watersheds located within the UIB, with a variability ranging from 0.10 to 0.32. The Elongation Ratio, denoted as ER, is a quantitative measure used to evaluate the extent of elongation or deformation experienced by a material under external stress. According to Strahler, the aforementioned ratio has a range of values spanning from 0.6 to 1.0 across different climatic and geologic categorizations. The improvement of watershed slope classification can be achieved through the utilization of the elongation ratio index. The current index categorizes slopes based on their elongation values, including circular slopes (0.9-0.10), oval slopes (0.8-0.9), less elongated slopes (0.7-0.8), elongated slopes (0.5-0.7), and very elongated slopes (< 0.5). Table 9 contains the statistical data regarding the elongation ratio. The Reynolds Number (RN) of the subbasins in Gilgit, Hunza, Gorband, Brandu, Panjkora, and Bara is less than 0.7. This observation suggested that the subbasins being studied exhibit an elongated shape with significant differences in elevation and steep slopes. The research findings indicate that there will be a reduction in travel time, enhanced concentration levels, decreased setbacks, and a decrease in the frequency of flood peaks. The subbasins that remain exhibit values below 0.5, indicating their elongated nature and vulnerability to erosion and the accumulation of silt.

The Compactness Coefficient, denoted as C, is a quantitative measure employed to assess the circularity of a basin. The observation of a circular basin exhibiting the minimum time of concentration before the initiation of peak flow within the basin has been documented. A Coefficient of Circularity (CC) equal to 1 signifies that the basin exhibits optimal circular attributes. A credit card number that exceeds 1 signifies an increased degree of departure from the circular characteristics of the basin. The assigned values for each subwatershed exhibit variation, ranging from 1.79 for Brandu to 3.13 for Shyok, as illustrated in Table 9. Consequently, it may be inferred that the Shyok subbasin exhibits the most pronounced departure from a circular morphology, suggesting that it will experience a more prolonged duration of concentration before attaining its maximum flow rate in comparison to the remaining subbasins.

The mathematical definition of the constant denoting channel maintenance, sometimes written as C, is the reciprocal of the Drainage Density (DD). This statistical measure calculates the necessary extent of the drainage area to sustain a predetermined length of a canal. The results of the current investigation demonstrated that variable C exhibits a variety of values, specifically ranging from 4.32 for Kanshi to 5.65 for Gilgit, as depicted in Table 9. The Kanshi, Soan, and Haro subbasins exhibit distinct features such as the presence of soils with poor resistivity, little vegetation, and rugged topography.

The shape index, denoted as S𝑤, is a quantitative metric employed to evaluate the shape characteristics of an object. The arrangement of a drainage basin is a significant factor in influencing the extent of water and sediment flow, as well as the size and topographic variations of the basin. The form index values for the sub-watersheds within the research region exhibit a notable disparity, with Gilgit recording a value of 3.52 and Kunar registering a value of 12.50, as depicted in Table 9. Within the context of surface water, it is apparent that Gilgit demonstrates a comparatively lower basin lag time, whereas Kunar exhibits a greater basin lag time.

Table 9: Shape characteristics (areal aspects) of mountainous watersheds of UIB, Pakistan.

Relief Dimensions:

The morphometric examination of a basin encompasses the evaluation of several relief characteristics, such as topography, relief ratio, relative relief, and roughness number. Table 10 displays the relief characteristics of each subbasin. The subject matter under consideration refers to the discipline of topography. The UIB exhibits an elevation variation spanning from 215m to 8566m above Mean Sea Level (MSL). The influence of altitude on meteorological variables, particularly temperature and snow accumulation, is widely acknowledged in scholarly discussions. The impact of changes in elevation on the processes of snowmelt and snow accumulation within mountainous watersheds has considerable importance. One potential strategy for enhancing simulation efficiency involves the subdivision of watersheds into distinct height bands, particularly in cases where there are notable changes in elevation and complex topographical features. The assessment of the distribution of the basin's area across different elevation classes among the 21 sub-basins was conducted and visually depicted in Figure 5. Figure 6 (See at the end of Paper) illustrates the geographical attributes of each subbasin.

The RR is a quantitative measure that assesses the vertical disparity between the maximum elevation observed inside a specific hydrological basin and the minimum height situated on the valley bottom. The topographic variation of the river basin, ranging from 0.53 km to 7.22 km, is a crucial factor to consider in this particular situation. The concept pertains to the quantitative assessment of the collective magnitude of incline shown by a hydrological basin. Moreover, it serves as a dependable indicator of the magnitude of erosion phenomena taking place on the inclines of the basin. There is typically a positive relationship between the Hydraulic Radius (HR) and the decrease in drainage area and size of a given drainage basin. The results of the current investigation indicate that the Rh values, as presented in Table 10, display variation across different geographic regions. In the Shyok region, the least observed value of HR is recorded as 0.01, while the highest reported value is documented as 0.074 in Gorband. Elevated levels of HR values indicate the existence of significant erosion processes. The findings of this study suggest that Gorband and Astore exhibit a higher vulnerability to erosion relative to Shyok, based on a single criterion used to assess erosion severity in the subwatersheds of the studied area.

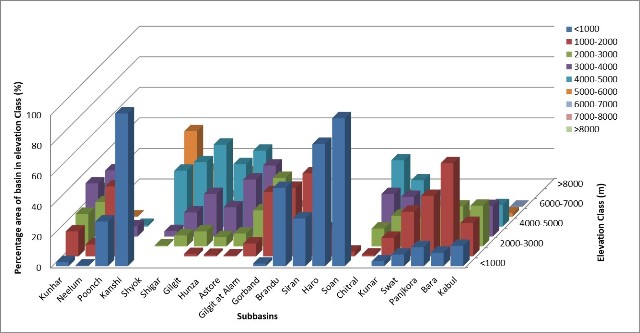
Figure 5: Percentage area of subbasins in various elevation classes.

Table 10: Maximum & minimum elevation, basin relief, relief ratio, relative relief, and ruggedness numbers of mountainous watersheds of UIB, Pakistan.

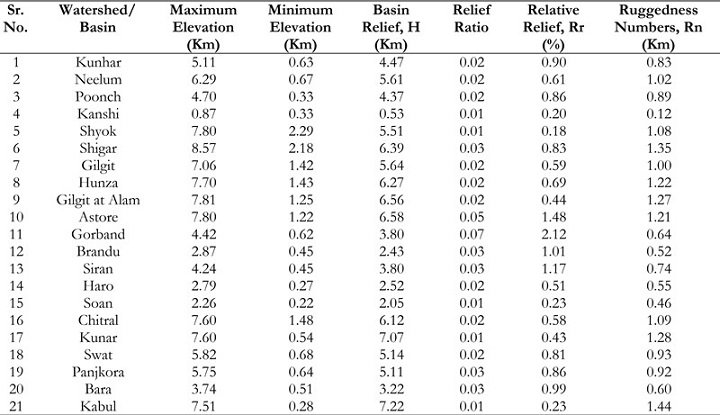
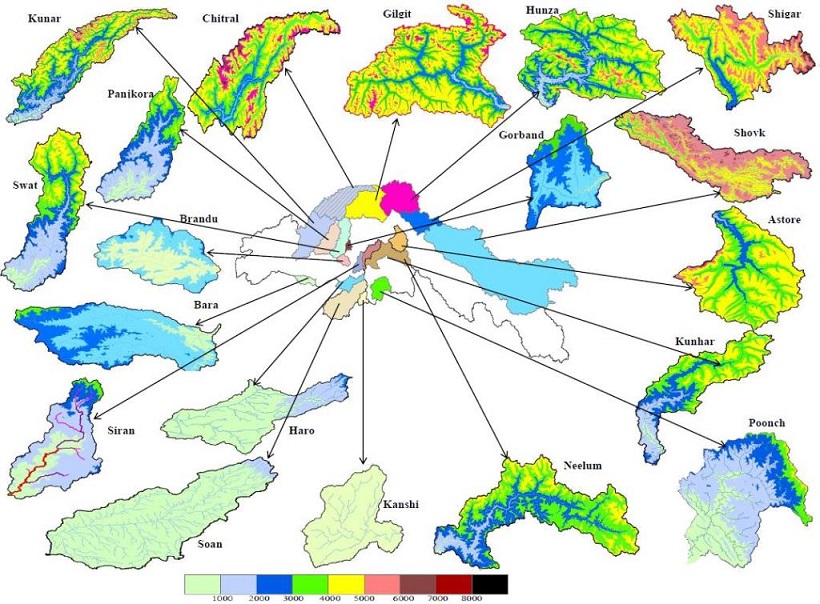
Figure 6: Topography of subbasins of Indus Bain Basin (IBB), Pakistan. (Elevation is in meter unit from above MSL)

The Ruggedness Number (Rn) is a quantitative metric employed to evaluate the level of structural complexity exhibited by a specific topography, taking into account factors such as variations in elevation and the density of water channels. Furthermore, this suggested that the region is prone to soil erosion. The results reported in Table 10 of the current study revealed that Kanshi and Soan display the lowest roughness values (𝑅𝑛 = 0.12 and 0.46, respectively), while Kabul exhibits the highest roughness value (𝑅𝑛 = 1.44). The findings suggest that the subwatershed of Soan exhibits the lowest susceptibility to erosion, whereas the subwatershed of Kabul demonstrates the highest vulnerability relative to all other sub-watersheds within the examined region.