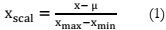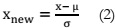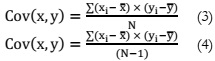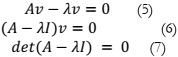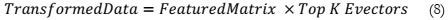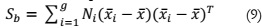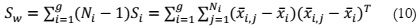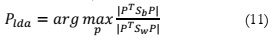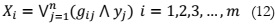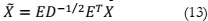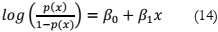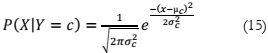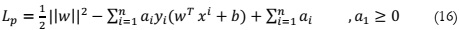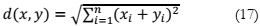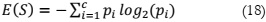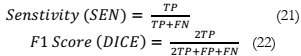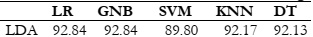E-ISSN:2709-6130
P-ISSN:2618-1630

Research Article

International Journal of Innovations in Science & Technology

2023 Volume 5 Number 4 Oct-Dec

An Optimal Feature Extraction Technique for Glioma Tumor Detection from Brain MRI

Khalid. A. R1, Suhail. Z1, Danish. H. F2

1 Department of Computer Science, University of the Punjab, Lahore, Pakistan.

2 Department of Computer Science, University of Engineering and Technology, New Campus, Lahore, Pakistan.

Abstract
A brain tumor is defined by the uncontrolled proliferation of brain tissue cells, defying the typical cellular regulation mechanisms governing growth. The most significant challenge associated with brain tumors lies in their timely diagnosis and accurate stage determination. Accurate detection of tumors from MRI scans can not only assist doctors in their examination but also provide crucial information for appropriate and timely treatment decisions. In this paper, a comprehensive analysis is presented based oncomparisons between state-of-the-art dimensionality reduction and classification algorithms. We useda dataset containing brain MRI scans, including both tumor and non-tumor cases, which wassplit into training and testing sets. After preprocessing the data, we implementedfour feature extraction algorithms to obtain different sets of features. Consequently, these sets of features were used to train five classifiers to analyze the accuracy. Based on these results, optimal feature extraction and brain tumor classification technique is selected. The results indicate that the Linear Discriminant Analysis (LDA) technique extracted highly informative features, leading to an impressive accuracy of 92.84%. This highlights the effectiveness of LDA in significantly enhancing the performance of the brain tumor classification process, making it the prime choice for feature extraction that aligns seamlessly with the research's intuition. It has higher accuracy with all the classifiers.

Keywords: Glioma Tumor, Classification, Feature Extraction, Dimensionality Reduction, Feature Selection, and Linear Discriminant Analysis.

Corresponding Author How to Cite this Article
Abdul Rahman Khalid, Department of Computer Science, University of the Punjab, Lahore, Pakistan.
 Abdul Rahman Khalid, Zobia Suhail, and Hafiz Muhammad Danish, An Optimal Feature Extraction Technique for Glioma Tumor Detection from Brain MRI. IJIST. 2023 ;5(4):562-575 https://journal.50sea.com/index.php/IJIST/article/view/558

Introduction

A brain tumor represents an unusual proliferation of cells within the brain, with the potential to be either cancerous (malignant) or non-cancerous (benign). These tumors can originate from various cell types in the brain and can impact a person's well-being, contingent upon their location, size, and characteristics. Malignant brain tumors are generally more aggressive, with the capacity to metastasize to other regions of the brain or the central nervous system. Conversely, benign brain tumors, although not inclined to spread, can still cause health issues if they increase in size and exert pressure on the surrounding brain tissue. Gliomas, for instance, result from the uncontrolled growth of glial cells that support nerves and the nervous system's function. Gliomas are generally malignant, although some may exhibit slow growth [3]. In 2020, primary brain cancer was the leading cause of death for 251,329 individuals [4]. The main issue contributing to this mortality rate is the late detection and classification of cancer [5]. In this research, we aimed to identify the most suitable method for efficiently classifying the tumor from MRI scans. In order to accomplish this, a combination of data pre-processing techniques was employed, which was subsequently followed by data transformation. However, we encountered certain challenges with data transformation, including dealing with a large dataset and irrelevant features. To address these issues, we employed a strategy known as feature extraction, which modifies the original data space to create new features. The main aim of these novel features was to enhance the distinction between various tumor categories and depict the issue in reduced-dimensional spaces. The experimental findings suggest improved classifier performance following feature extraction, particularly for datasets with a high dimensionality.

In this study, four dimensionality reduction algorithmsβ€”Principal Component Analysis (PCA), Independent Component Analysis (ICA), Linear Discriminant Analysis (LDA), and Factor Analysis (FA)β€”are implemented. However, LDA is not included in the feature extraction process since it autonomously selects features based on its underlying model, without requiring a predefined number of features. Instead, sets of 50, 100, 200, 250, and 300 features are extracted from the data using PCA, ICA, and FA. Furthermore, to evaluate the effectiveness of the extracted features, various state-of-the-art classifiers, including Logistic Regression (LR), Gaussian Naive Bayes (GNB), Support Vector Machine (SVM), K Nearest Neighbor (KNN), and Decision Tree (DT) are trained on each set of 50, 100, 200, 250, and 300 features.

Objectives:

This is a comparative study with the primary objective of identifying the optimal feature extraction technique capable of yielding features that achieve a classification accuracy of 90% or higher for tumor classification.

Novelty Statement:

The key contribution of this research lies in conducting a comprehensive analysis to identify the optimal feature extraction technique. Several experiments were conducted, and it is observed that all feature extraction techniques demonstrated robust performance when paired with specific classifiers. However, the effectiveness of each feature extraction method varies depending on the chosen classifier. For instance, PCA exhibited excellent performance when used with SVM, whereas it yielded the poorest results when paired with GNB. Our findings demonstrated that LDA consistently achieves accuracy levels exceeding 90% when employed with various classifiers. This robust performance underscores LDA's suitability for accurate and efficient feature extraction in brain tumor classification. We anticipate that both researchers and medical practitioners will find our results valuable in their pursuit of highly accurate brain tumor classification, encompassing a wide range of tumor types, including Gliomas, Pituitary, Meningioma, and Glioblastoma, all attainable within seconds.

The remainder of the paper is organized as follows: In section 2, the related background is briefly described. In section 3, the material and methods are described. Section 4 presents an analysis of experimental results and comparisons. Finally, we conclude with the research findings.

Related Work:

Charfi et al. [6] conducted a comprehensive assessment of various studies related to brain tumor detection and introduced an innovative hybrid approach for analyzing MRI brain images. This approach employs discrete wavelet transform for feature extraction, incorporates automated thresholding for image segmentation and region of interest identification. Subsequently, PCA is employed to reduce the dimensionality of the wavelet coefficients, leading to a more efficient and accurate classifier. The method demonstrated a commendable accuracy of 90%.

Ural et al. [7] introduced an innovative approach for brain tumor detection, leveraging probabilistic neural networks and advanced image processing techniques. Their method involved a sequence of operations, including k-means and fuzzy-mean clustering, thresholding, and level segmentation, to isolate the tumor region within the brain images. Subsequently, the utilization of probabilistic neural networks led to an impressive 90% accuracy in brain tumor detection.

Sudharani et al. [8] presented a method for brain tumor detection and the assessment of its statistical parameters, which also aids in sensitivity determination and similarity index calculation. Their technique involved adjustments to image brightness, image re-sampling, color plane extraction for thresholding, and advanced morphological processes for information extraction from images. This method achieved an accuracy of 89.2%.

Sukumar et al. [9] introduced an innovative approach for brain tumor detection using MRI images. Their methodology comprised sequential steps, starting with image segmentation to identify and isolate the tumor region of interest. Subsequently, they applied PCA for feature extraction and employed a SVM as the classifier to distinguish between benign and malignant tumors based on the extracted features. Experimental results underscored the superiority of their proposed technique in comparison to previous methods for brain tumor detection. This study's findings highlight the considerable performance improvement achieved through the combination of image segmentation, PCA-based feature extraction, and SVM classification, representing a promising advancement in medical image analysis.

Paul et al. [10] introduced a brain tumor diagnosis method based on brain MRI images. They utilized two types of neural networks: a fully connected neural network and a convolutional neural network for image classification. To enhance the classification performance, additional tests were performed on these two groups by incorporating supplementary information into the original 512x512 axis images. Notably, their proposed approach exhibited exceptional accuracy, surpassing well-trained neural networks with an impressive accuracy rate of 91.43%.

Material and Method

An overview of the procedure is described in Figure 1, while the details are expounded in the subsequent subsections:

Data Collection:

A dataset of brain MRIs, published by Kaggle [1][2], is utilized in this study. A total of 4082 MRIs, with 2795 images are used for training and 1287 used for testing purposes. The dataset is organized into two classes: non-tumorous (0) and tumorous (1), allowing us to perform binary classification tasks for brain tumor detection. Figure 2 showcases sample MRI scans depicting glioma tumors, which are among the most dangerous types of brain tumors. Conversely, Figure 3 displays samples of non-tumor MRI scans.

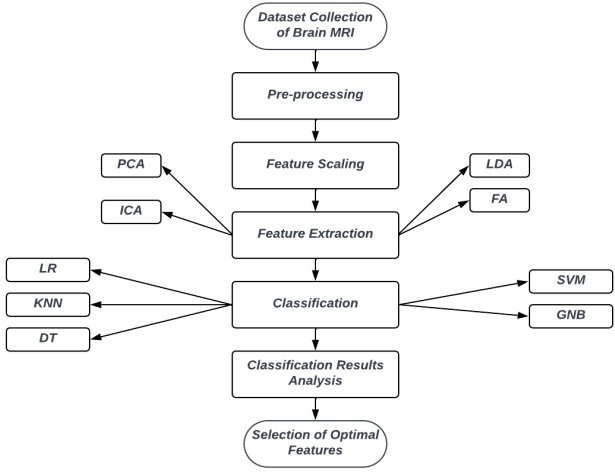
Figure 1: Block diagram of our research methodology.

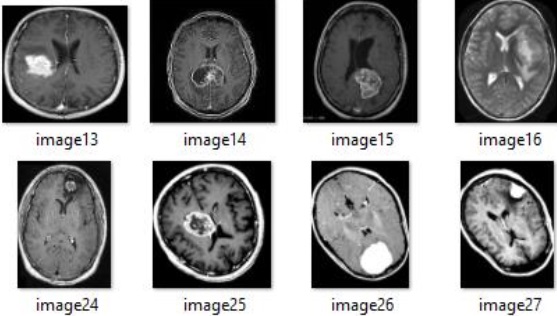
Figure 2: Samples of brain MRI scans with Glioma tumor.

Image Pre-processing:

The dataset contained images of various sizes, necessitating the resizing of all images to a standardized dimension of 200x200 pixels. Furthermore, all images were converted to grayscale.

Feature Scaling:

Feature scaling involves the standardization of independent variables or features within the data. Mean normalization, in this context, is a step in which a dataset obtained from the previous stage is processed as follows:

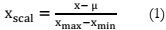
Feature Extraction:

Feature extraction is the procedure of converting unprocessed data into numerical features. These numerical features are derived from the original dataset and can often yield superior results compared to the utilization of raw data in machine learning applications, as emphasized in [11]. This research employs various feature extraction techniques, including PCA, LDA, FA, ICA, and a combination of PCA and LDA.

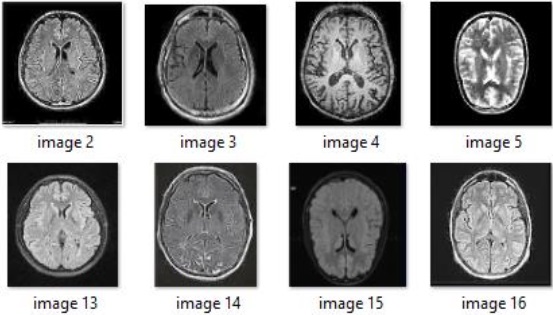
Figure 3: Samples of brain MRI scans without tumor.

Principal Component Analysis:

PCA [12] is recognized as one of the most potent feature extraction techniques. It involves the utilization of eigenvalues from a covariance matrix to identify the corresponding eigenvectors. This process begins by extracting the largest variance, which is added as the first factor. Subsequently, the variance explained by the first factor is subtracted, allowing for the extraction of the highest variance for the second component. This iterative process leads to the final factor. PCA fundamentally converts a matrix with n features into a new dataset with fewer than n features by extracting the most essential information from the original features. The steps of PCA include:

Apply equation (2) to standardize the dataset.

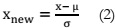
Calculation of the correlation matrix for both the population and sample using (3) and (4) respectively.

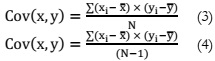
Calculation of eigenvalues and eigenvectors for the covariance matrix using (5), (6), and (7).

1. Sorting eigenvalues based on the eigenvectors that they belong to.

2. Picking k eigenvalues from a matrix of eigenvectors.

3. Performing a transformation on the original matrix using (8).

Linear Discriminant Analysis:

In the realm of machine learning and pattern classification, LDA [13] is an essential preprocessing step involves supervised dimensionality reduction. LDA reduce the number of dimensions by transferring features from a higher-dimensional space to a lower-dimensional one, effectively eliminating redundant and interdependent features. To obtain linear discriminants several sequential steps are executed.

The first step involves calculating the between-class variance, representing the separability between different classes, expressed as:

The second step is dedicated to determining the within-class variance, which quantifies the difference between each class's mean and the individual data samples, defined as:

The final stage revolves around identifying the lower-dimensional space that maximizes the variability among classes while reducing the variance within classes. This is achieved by determining P, which represents the projection of the lower-dimensional space :

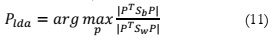
Independent Component Analysis:

ICA [14] is another dimensionality reduction approach. In ICA, data variables in the model are linear combinations of latent variables that are not yet identified, referred to as independent components, as they exhibit non-Gaussian characteristics and are mutually independent. ICA serves two primary purposes: reducing information redundancy and increasing non-Gaussianity. It plays a vital role in blind signal separation and finds numerous real-world applications. ICA is intricately associated with the search for the fundamental data representation. Binary ICA represents a specific variant, where both the sensors and signal sources are binary, and the observations consist of disjunctive combinations of independent binary sources. The mathematical representation for this is given as:

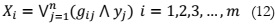
The reduction of eigenvalues in a signal's covariance matrix is essentially a process for signal purification. The relevant mathematical equation is as follows:

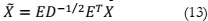
In this equation, E represents a matrix of eigenvectors, and D is a diagonal matrix of eigenvalues. The steps involved in ICA are as follows:

1. Centering the data by subtracting the mean.

2. Applying whitening to the centered data using the mentioned technique.

3. Initializing the matrix w with random values.

4. Calculate the updated value of w.

5. Normalizing the updated value of w.

6. Returning to step 4 if the algorithm is not yet converged.

Factor Analysis:

FA [15] serves the purpose of reducing a large number of variables into a smaller, more manageable set. It can be utilized in various tasks, including linear projection and matrix factorization. By condensing the original variables into a reduced set referred to as factors, FA, a linear modeling technique, seeks to capture the common variability among observed and interconnected variables. In FA, a latent variable referred to as a factor explains the correlations among observable variables. Each factor represents a distinct source of variation in the observed variables. The process of factor analysis typically involves the following steps:

1. Checking the factorability of the data.

2. Determining the appropriate number of factors to retain.

3. Interpreting and understanding the meaning of the identified factors.

Training Classifiers:

A classifier is an algorithm designed to automatically categorize data into one or more predefined sets of categories. Machine learning encompasses a variety of classifiers, and in this research, the following classifiers are utilized, each with its respective description:

Logistic Regression:

Logistic regression, a classifier [16], is among the most commonly used machine learning algorithms in the category of supervised learning. It is employed for predicting a categorical dependent variable based on a given set of independent variables. Logistic regression is particularly useful when the objective is to forecast outcomes for a categorical dependent variable. The expression for logistic regression is as follows:

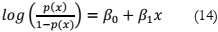
Gaussian Naive Bays:

Naive Bayes is a probabilistic machine learning approach widely applied in various classification tasks, built upon the foundation of Bayes' theorem [17]. An extension of Naive Bayes known as Gaussian Naive Bayes is employed, with the Gaussian (or normal) distribution being the simplest to implement. In this approach, other functions are used to estimate data distribution, necessitating the identification of mean and standard deviation values from the training data. The formula for the GNB algorithm is as follows:

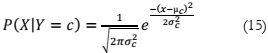
Support Vector Machine:

SVM, a supervised machine learning method [18], is employed for both classification and regression tasks, although it is more commonly associated with classification. SVM operates by partitioning data points into class attributes using a hyperplane. Each data point in this algorithm is represented as a point in n-dimensional space defined by specific coordinate values. The classification task involves identifying the hyperplane that effectively separates and distinguishes between two classes. The formulation of the Lagrange SVM is expressed as:

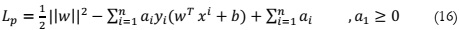
K Nearest Neighbor:

KNN, a widely adopted supervised machine learning approach for classification tasks [19], classifies data points based on the categorization of their nearest neighbors. The algorithm uses a similarity index computed from previously classified instances to determine the category of a new case. In essence, the method assesses an unknown item by examining the k closest neighbors that share similar characteristics based on the attributes used to describe the items. The neighbors' votes are then used to determine the classification. The mathematical formulation of KNN is as follows:

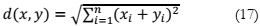
Decision Tree:

DT is utilized for both classification and regression tasks [20]. In classification, it is structured as tree-like models with discrete values for the target variable. DT employ diverse criteria to determine whether a node should be split into two or more sub-nodes. The creation of additional sub-nodes leads to an increase in their homogeneity or purity, with a focus on the desired parameter. In the context of binary classification, where there are two classes in the output, the first step involves calculating the probability of each class in the output (P(y+) and P(y-)), followed by:

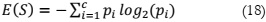
Evaluation Metrics:

In evaluating the performance of the model, four parameters are employed, namely accuracy , precision , sensitivity , and Dice. Accuracy is the most commonly used metric for assessing binary classification problems [21]. It is calculated as the percentage of correct predictions out of the total outcomes and can be computed as (19). Precision, on the other hand, quantifies how precise the classifier is in detecting true positive results and is given as (20).

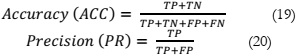
Sensitivity, as defined in (21), represents the rate of positive predictions. The F1 score, expressed as (22), is a weighted harmonic average of precision and recall, with values ranging between 0 and 1.

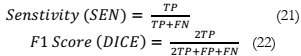
Result

Experiments and Results:

In this study, several experiments are performed on brain MRI scans, and the obtained results are thoroughly analyzed. The primary aim of these analyses is to identify the optimal feature extraction and classification techniques for accurately detecting brain tumors from MRI images.

Performance Evaluation of Feature Extraction Methods:

After conducting experiments involving various feature extraction techniques in combination with different classifiers, it became evident that the performance of these techniques varies depending on the choice of classifier, resulting in different accuracy levels. Notably, in our experimental evaluation, we observed that PCA, ICA, and FA, when used with their default feature counts, did not yield satisfactory performance. To address this issue, we decided to apply PCA, FA, and ICA with different feature counts: 50, 100, 200, 250, and 300. Subsequently, we subjected all the classifiers to evaluation using the aforementioned sets of extracted features. The results of these evaluations are detailed below, and they serve as the basis for selecting the optimal feature extraction technique.

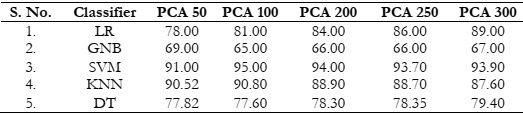
Results Comparison by Utilizing PCA:

The evaluation results are summarized in Table 1, revealing that the SVM and KNN classifiers delivered satisfactory performance. However, it's worth noting that as the number of features increased, the accuracy of SVM and KNN exhibited a declining trend, as depicted in Figure 4 (a). In contrast, logistic regression demonstrated an increase in accuracy with the growing number of features. It's important to highlight that not all classifiers were able to meet our anticipated accuracy criteria,

Table 1: Accuracy (%) comparison of classifiers using PCA.

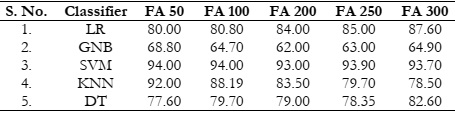
Results Comparison by Utilizing FA:

The utilization of FA with varying feature counts consistently resulted in favorable accuracy levels, particularly when applied in conjunction with SVM and KNN classifiers, as depicted in Figure 5 (a). It has the same issue, LR and GNB did not perform well in this scenario. Only SVM and KNN achieved the expected accuracy as shown in Figure 5 (b). The overall results comparison with FA is depicted in Table 2.

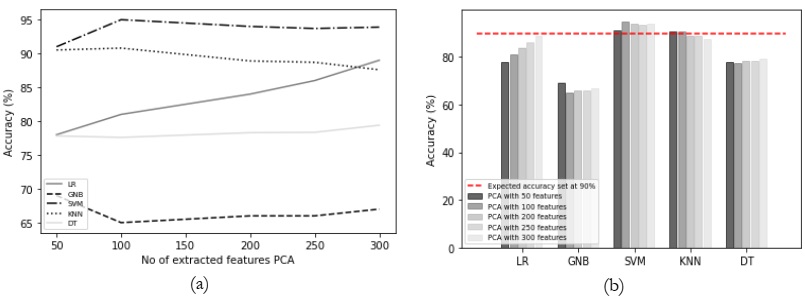
Figure 4: (a) Comparison between accuracy and number of extracted features using PCA and (b) accuracy comparison with the different classifiers using PCA.

Table 2: Accuracy (%) comparison of classifiers using FA.

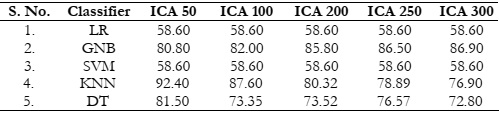
Results Comparison by Utilizing ICA:

ICA was employed with varying feature counts, and the associated results have been summarized in Table 3. However, it's worth noting that ICA did not outperform PCA, FA, and LDA in terms of achieving better results. Only the KNN classifier showed relatively good results with ICA, but its performance also exhibited a decline as the number of features increased, as indicated in Figure 6 (a). On the other hand, none of the other classifiers managed to attain satisfactory results, consistently falling short of the expected performance, as visualized in Figure 6 (b).

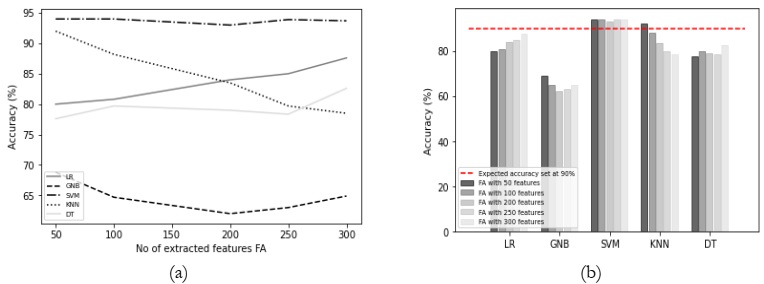
Figure 5: (a) Comparison between accuracy and number of extracted features using FA and (b) accuracy comparison with the different classifiers using FA.

Table 3: Accuracy (%) comparison of classifiers using ICA.

Results Comparison by Utilizing LDA:

LDA is used with the default number of features. It uses different formulas to extract features. When using LDA with default features, all classifiers achieve the expected accuracy, as shown in Figure 7. Furthermore, there is a minimal difference observed among the accuracies of the classifiers This demonstrates that it is an effective feature extraction technique capable of yielding improved results with any of the classifiers. The corresponding results are also shown in Table 4.

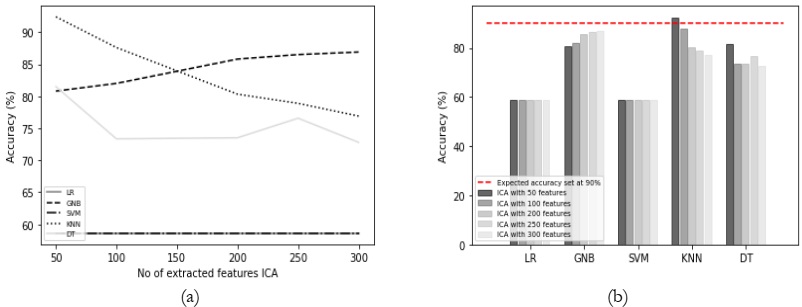
Figure 6: (a) Comparison between accuracy and number of extracted features using ICA and (b) Accuracy comparison with the different classifiers using ICA.

"π‘π‘œ π‘œπ‘“ π‘“π‘’π‘Žπ‘‘π‘’π‘Ÿπ‘’ = 𝑀𝑖𝑛 (π‘›π‘’π‘šπ‘π‘’π‘Ÿ π‘œπ‘“ π‘π‘™π‘Žπ‘ π‘ π‘’π‘  βˆ’ 1, π‘›π‘’π‘šπ‘π‘’π‘Ÿ π‘œπ‘“ π‘“π‘’π‘Žπ‘‘π‘’π‘Ÿπ‘’π‘ ) (23)"

Table 4: Accuracy (%) comparison of classifiers using LDA.

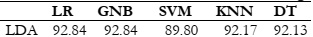
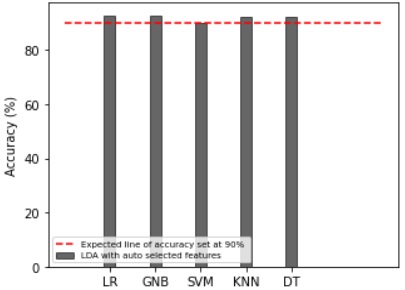
Figure 7: Accuracy comparison with the different classifiers using LDA.

Results Comparison by Utilizing Combined PCA and LDA:

In this approach, both PCA and LDA are combined, wherein PCA is applied with varying numbers of features, while LDA retains its default feature selection. This technique yielded the highest accuracy of 88.01%, with minimal variations among the accuracies of other classifiers, as indicated in Table 5. As presented in Figure 8 (a), the accuracy improved as the number of features increased. However, based on the results displayed in Figure 8 (b), it is noteworthy that LDA alone provides higher accuracy compared to the combined PCA and LDA approach. Therefore, LDA is considered the optimal choice for these classification tasks.

Table 5: Accuracy (%) comparison of classifiers combined PCA and LDA.

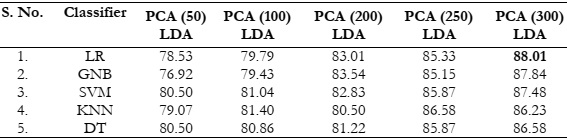
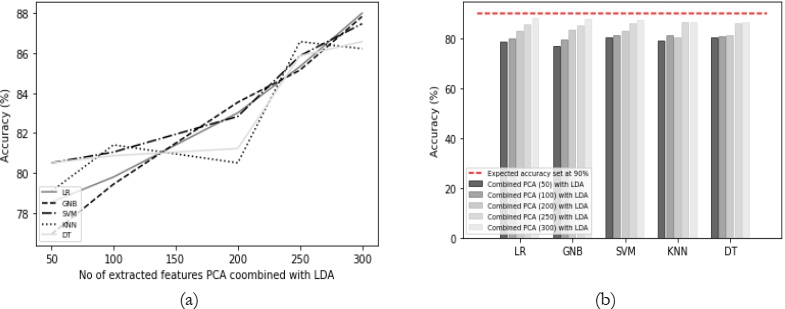
Figure 8: (a) Comparison between accuracy and number of extracted features using PCA combined LDA and (b) Accuracy comparison with the different classifiers using PCA combined LDA.

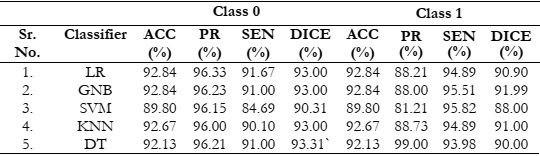
Table 6: Evaluation results of various classifiers with an optimal feature extraction technique LDA.

Discussion

The results of the study demonstrate that LDA is the most effective feature extraction technique, consistently yielding high-accuracy results in the classification of brain tumors, covering a diverse spectrum of tumor types such as Gliomas, Pituitary, Meningioma, and Glioblastoma. Glioma tumors are a group of primary brain tumors that originate from glial cells, which provide support and protection for neurons in the central nervous system. Gliomas are classified into various types and grades including low-grade (Grade I and II) and high-grade (Grade III and IV) based on their histological features and behavior. Pituitary tumors, also known as pituitary adenomas, are tumors that develop in the pituitary gland, a small gland located at the base of the brain. These tumors can vary in terms of their size, hormone secretion, and clinical features. Meningioma is a type of primary brain tumor that originates from the meninges, which are the protective membranes that surround the brain and spinal cord. Meningiomas are typically slow-growing and benign, but they can occasionally be malignant. Glioblastoma is the most invasive glial tumor because it grows rapidly and can damage other tissues due to poor prognosis.

The MRIs employed in this study were gathered as segments or sections from various sources of datasets. These chunks were based on both cancerous and non-cancerous images. A total of 4082 MRIs, with 2795 images are used for training and 1287 used for testing purposes. We standardized the image resolution by resizing all images to 200 by 200 pixels. Each image in the dataset is typically associated with one label. These labels denote the specific tumor type present (e.g., glioblastoma, meningioma, pituitary tumor, glioma tumor), or the absence of a tumor (i.e., normal brain images). It's worth noting that patient age and gender-related information is not available in the metadata utilized for our research.

We compared our proposed feature selection technique with state-of-the-art feature selection techniques including PCA, ICA, FA, Combined PCA-LDA. Furthermore, we not only obtained a varying number of features through extraction but also subjected these features to analysis by five different classifiers in order to assess the classification results. The evaluation results indicate that the proposed LDA technique extracted highly informative features, leading to an impressive accuracy of 92.84%.

Our evaluation of the proposed technique focused exclusively on MRI scans, without considering other imaging modalities such as ultrasound, X-rays, or CT scans. We employed a set of five well-established classifiers, including logistic regression, support vector machine, decision trees, Gaussian Naive Bayes, and K Nearest Neighbor, for the classification process. The study concentrated on the classification of four specific tumor types: Gliomas, Pituitary tumors, Meningioma, and Glioblastoma.

In real world, brain tumor classifiers are implemented in various healthcare settings, including hospitals, cancer centers, and telemedicine applications, where they assist radiologists and clinicians in diagnosing and managing brain tumors, ultimately improving patient care and treatment planning. They are also used in clinical trials, educational platforms, and resourcelimited areas to enhance diagnostic accuracy. Additionally, these classifiers are integrated into radiology software, medical imaging workstations, and teleradiology services, while research institutions, startups, and government health initiatives utilize them for research, development, and healthcare system improvement.

Looking ahead, this technique shows potential for more extensive applications, encompassing the classification of diverse types of cancer, including lung, breast, and liver cancer. This approach is expected to yield improved results across these diverse datasets, potentially leading to earlier cancer diagnoses. Additionally, exploring the integration of LDA as a feature extraction method in conjunction with other classifiers like convolutional neural networks and Bayesian quadratic classifiers on brain MRI datasets could be a valuable avenue for investigation and evaluation. Furthermore, it may be worthwhile to explore alternative feature extraction techniques, such as local binary patterns and log Gabor algorithms. To enhance the accuracy of this technique in future research, additional preprocessing steps on the dataset can also be considered.

Conclusion

The objective of the study was to identify the most effective feature selection technique. To accomplish this, several experiments were conducted using the Glioma tumor dataset sourced from Kaggle. To improve the performance, we extracted several feature counts, including 50, 100, 200, 250, and 300, and employed state-of-the-art classifiers. Unfortunately, the results of the comparisons did not meet our expectations. However, the breakthrough came when we employed LDA for feature extraction. All the classifiers exhibited exceptional performance and consistently achieved accuracy levels exceeding 90%, making them indisputable frontrunners in this competition. Thus, we propose LDA as an optimal feature selection technique for brain MRI classification.

Ethics approval and consent to participate:

Formal consent is not required in this type of study.

Availability of dataset and materials:

The data supporting the findings of the article is available at https://www.kaggle.com/dsv/2645886 and https://www.kaggle.com/dsv/1183165 [1][2].

Acknowledgement: The authors acknowledge all the efforts of Nickparvar [1] and Bhuavaji et al. [2] for generously providing the datasets used in this study. Their contribution has been invaluable to the successful completion of our research.

Project Detail: Nil

Conflict of Interest: The authors declare that they have no conflict of interest.

Reference

[1] β€œBrain Tumor MRI Dataset.” https://www.kaggle.com/datasets/masoudnickparvar/brain-tumor-mri-dataset (accessed Nov. 02, 2023).

[2] β€œBrain Tumor Classification (MRI).” https://www.kaggle.com/datasets/sartajbhuvaji/brain-tumor-classification-mri (accessed Nov. 02, 2023).

[3] B. Ilhan, P. Guneri, and P. Wilder-Smith, β€œThe contribution of artificial intelligence to reducing the diagnostic delay in oral cancer,” Oral Oncol., vol. 116, p. 105254, May 2021, doi: 10.1016/J.ORALONCOLOGY.2021.105254.

[4] A. Osman and B. Alsabbagh, β€œImage-classification for Brain Tumor using Pre-trained Convolutional Neural Network”.

[5] M. Westphal and K. Lamszus, β€œThe neurobiology of gliomas: from cell biology to the development of therapeutic approaches,” Nat. Rev. Neurosci. 2011 129, vol. 12, no. 9, pp. 495–508, Aug. 2011, doi: 10.1038/nrn3060.

[6] L. R. S. Charfi, R. Lahmyed, β€œA novel approach for brain tumor detection using neural network,” Int. J. Res. Eng. Technol., vol. 2, no. 7, pp. 93–104, 2014.

[7] B. Ural, β€œA Computer-Based Brain Tumor Detection Approach with Advanced Image Processing and Probabilistic Neural Network Methods,” J. Med. Biol. Eng., vol. 38, no. 6, pp. 867–879, Dec. 2018, doi: 10.1007/S40846-017-0353-Y/METRICS.

[8] K. Sudharani, T. C. Sarma, and K. S. Prasad, β€œAdvanced Morphological Technique for Automatic Brain Tumor Detection and Evaluation of Statistical Parameters,” Procedia Technol., vol. 24, pp. 1374–1387, Jan. 2016, doi: 10.1016/J.PROTCY.2016.05.153.

[9] A. S. A. and P. Augustine, β€œEfficient brain tumor classification using PCA and SVM,” Int. J. Res. Eng. IT Soc. Sci., vol. 7, pp. 1–7, 2017.

[10] β€œDeep learning for brain tumor classification.” https://www.spiedigitallibrary.org/conference-proceedings-of-spie/10137/1/Deeplearning-for-brain-tumor-classification/10.1117/12.2254195.full (accessed Nov. 02, 2023).

[11] I. Guyon and A. Elisseefl, β€œAn introduction to feature extraction,” Stud. Fuzziness Soft Comput., vol. 207, pp. 1–25, 2006, doi: 10.1007/978-3-540-35488-8_1/COVER.

[12] R. Bro and A. K. Smilde, β€œPrincipal component analysis,” Anal. Methods, vol. 6, no. 9, pp. 2812–2831, Apr. 2014, doi: 10.1039/C3AY41907J.

[13] P. Xanthopoulos, P. M. Pardalos, and T. B. Trafalis, β€œLinear Discriminant Analysis,” pp. 27–33, 2013, doi: 10.1007/978-1-4419-9878-1_4.

[14] J. V. Stone, β€œIndependent component analysis: an introduction,” Trends Cogn. Sci., vol. 6, no. 2, pp. 59–64, 2002.

[15] N. Khosla, β€œDimensionality reduction using factor analysis,” Griffith Univ. Aust., 2004.

[16] J. R. Lambert and E. Perumal, β€œOptimal Feature Selection Methods for Chronic Kidney Disease Classification using Intelligent Optimization Algorithms,” Recent Adv. Comput. Sci. Commun., vol. 14, no. 9, pp. 2886–2898, Aug. 2020, doi: 10.2174/2666255813999200818131835.

[17] H. Kamel, D. Abdulah, and J. M. Al-Tuwaijari, β€œCancer Classification Using Gaussian Naive Bayes Algorithm,” Proc. 5th Int. Eng. Conf. IEC 2019, pp. 165–170, Jun. 2019, doi: 10.1109/IEC47844.2019.8950650.

[18] W. S. Noble, β€œWhat is a support vector machine?,” Nat. Biotechnol., vol. 24, no. 12, pp. 1565–1567, Dec. 2006, doi: 10.1038/NBT1206-1565.

[19] Y. Liao and V. R. Vemuri, β€œUse of K-Nearest Neighbor classifier for intrusion detection,” Comput. Secur., vol. 21, no. 5, pp. 439–448, Oct. 2002, doi: 10.1016/S0167- 4048(02)00514-X.

[20] A. J. Myles, R. N. Feudale, Y. Liu, N. A. Woody, and S. D. Brown, β€œAn introduction to decision tree modeling,” J. Chemom., vol. 18, no. 6, pp. 275–285, Jun. 2004, doi: 10.1002/CEM.873.

[21] M. Hossin and Sulaiman, β€œA REVIEW ON EVALUATION METRICS FOR DATA CLASSIFICATION EVALUATIONS,” Int. J. Data Min. Knowl. Manag. Process, vol. 5, no. 2, 2015, doi: 10.5121/ijdkp.2015.5201.