Comparative Analysis of Lossless Image Compression Algorithms

Umer Ijaz; Abubaker Ijaz; Ali Iqbal; Fouzia Gillani; Muzammil Hayat

Comparative Analysis of Lossless Image Compression Algorithms

Ijaz. U¹, Ijaz. A², Iqbal. A¹, Gillani. F³, Hayat. M¹

¹ Department of Electrical Engineering & Technology, GC University, Faisalabad

² Director Development, WASA, Faisalabad

³ Department of Mechanical Engineering and Technology, GC University, Faisalabad

Abstract
This research paper conducts a comprehensive analysis of three key lossless image compression algorithms: Run-Length Encoding (RLE), Burrows-Wheeler Transform (BWT) and Differential Pulse Code Modulation (DPCM). The increasing demand for efficient image storage and transmission necessitates a thorough examination of these algorithms. Lossless compression plays a crucial role in diminishing data redundancy while safeguarding the integrity and quality of images. The study encompasses data collection, performance metrics, and algorithm evaluation. Results reveal the strengths and weaknesses of each algorithm. RLE excels in image quality preservation but may not achieve the highest compression ratios. DPCM provides a compromise between resource-efficient compression and image fidelity. BWT offers a competitive balance between compression efficiency and image quality. Based on the comprehensive analysis of three key lossless image compression algorithms, it was observed that BWT emerges as a versatile choice that offers competitive compression while maintaining reasonable image quality. However, when choosing the most suitable algorithm, it is essential to consider specific application requirements, including the desired level of image quality preservation and the availability of computational resource.

Keywords: Lossless Image Compression, Run-Length Encoding, Burrows-Wheeler Transform, Differential Pulse Code Modulation, PSNR, SSIM, MSE, RMSE, Bitrate, Computational Complexity.

Corresponding Author	How to Cite this Article
Umer Ijaz, Department of Electrical Engineering & Technology, GC University, Faisalabad	Umer Ijaz, Abubaker Ijaz, Ali Iqbal, Fouzia Gillani, Muzammil Hayat, Comparative Analysis of Lossless Image Compression Algorithms. IJIST. 2023 ;5(4):548-561 https://journal.50sea.com/index.php/IJIST/article/view/559

Introduction

The ever-increasing demand for efficient image storage and transmission has led to the development of various image compression techniques. Among these, lossless image compression algorithms hold significance due to their ability to compress images without any loss of information. This compression technique [1] is crucial when there is a requirement to transmit data over the Internet or store it on a digital device while ensuring that no information is lost in the process. Image compression helps to store, categorize, and recognize images by eliminating unnecessary data in the image. This technique [2] is important when we want to save storage space or make data transfer faster. The proliferation of social media and digital networks has increased our interaction with numerous images on a daily basis. However, larger images demand more time for transmission and storage. High-quality images, in particular, require significant storage space and bandwidth. Lossless image compression is important in fields like remote sensing, healthcare, security, and military. We need to keep image quality high to avoid mistakes in analysis or diagnosis. In today's fast-paced world of technology [3], we need data to move quickly, and this is where compression algorithms come into play. However, keeping the data quality intact while compressing is a big challenge. Over the years, international organizations [4] have produced many strategies for data compression. However, there is not a one-size-fits-all solution. The effectiveness of an algorithm for lossless image compression is typically measured using the compression ratio (how much the data is reduced in size), and the time it takes to encode and decode the data [5]. The true challenge lies in selecting the most suitable algorithm from a multitude of options, tailored to meet the specific requirements of a given application. It takes a good, hard look at the data from all angles and recommends the best algorithm for each type of data. Lossless image compression [6] is very important when we want to save or send images without losing any details. In image processing, the two [7] most crucial things are how clear the image is (resolution) and how fast we can collaborate with it (processing speed). Managing multimedia data that is both high-quality and massive can be quite a challenge[8]. In the realm of digital technology, reducing file sizes holds great significance. Large files consume substantial storage space and result in prolonged transfer times across the Internet. Therefore, innovative methods for compressing images, conserving storage capacity, and enhancing data transmission speed are imperative [9]. Effectively handling and sharing this data can pose a significant hurdle [10], whether it involves storage on your computer or transmitting it via the internet. Transmitting images from space can present a substantial challenge due to inherent limitations on data transmission and storage. Conventional image compression techniques may not consistently perform optimally for the images, given the constraints related to memory, bandwidth, energy, and processing capabilities.

Image compression plays a pivotal role in a variety of domains, including business, research, defense, and healthcare. Bulky image files can be burdensome, as they demand extensive processing time and a significant amount of storage space. Therefore, the significance of image compression lies in its ability to maintain image quality while making them more manageable for practical applications in the real world. The mechanism of compression involves the elimination of surplus components from the image. Several types of redundancies exist with certain components are overly duplicated, some image areas contain akin pixels that do not necessitate repetition, and occasionally, non-essential visual details are disregarded. All these excesses can be pruned without significantly detracting from the image's integrity. This literature review provided valuable insights into the progress and breakthroughs in image compression algorithms. The findings from these studies played a crucial role in informing and substantiating our comparative analysis of Run-Length Encoding (RLE), (BWT) and (DPCM), in relation to their compression performance, visual fidelity and minimized distortion. The knowledge acquired through the literature review served as a robust basis for the subsequent sections of this research paper. This paper focuses on the comparative analysis of three widely used lossless image compression algorithms: RLE, BWT and DPCM.

Objectives:

The main objective of this research paper is to compare different algorithms for compressing images without losing any data to evaluate various performance metrics that can provide practical recommendations for decision makers outlined a comprehensive methodology and implementation plan. It emphasize the significance of image compression in today’s technology and communication. These objectives contribute to the field of image compression and its broader applications in science and technology.

Novelty Statement:

This research study is novel for its examination of three significant lossless image compression algorithms: RLE, BWT, and DPCM. While previous studies have examined these algorithms individually. However, this paper contributes by systematically comparing their performance using various metrics. This approach enhances our understanding of image compression in situations and provides valuable insights to those involved in decision making. The significance of this research lies in its evaluation of lossless image compression algorithms addressing the need for efficient image compression in real world scenarios while offering useful guidance for decision makers. The inclusion of a range of performance metrics and a clear methodology further enhances the significance of this contribution to the field of image compression and its applications in science and technology.

Comparative Analysis of Lossless Image Compression Algorithms:

The paper systematically conducts a comprehensive analysis of three prominent lossless image compression algorithms: RLE, BWT and DPCM. This study distinguishes itself through its innovative approach. While previous research typically focused on examining these algorithms individually, this paper stands out by conducting a comprehensive comparison of their performance across a range of critical metrics. This comparative analysis offers a fresh and distinctive viewpoint on their respective advantages and limitations, enabling better-informed choices when deciding on compression methods.

Addressing the Escalating Demand for Efficient Image Compression:

In a contemporary context marked by the ever-growing demand for efficient image storage and transmission, driven by the proliferation of digital images, this paper takes on the role of addressing a highly relevant and practical problem within the field of image processing and compression. This approach helps to solve real-world data management difficulties and contributes significantly to the continued research and progress of image compressing algorithms.

Incorporation of Multiple Performance Metrics:

The research paper's distinctiveness lies in its thorough examination of three compression algorithms, utilizing a diverse set of performance metrics, such as PSNR, SSIM, MSE, RMSE, Bitrate, and Computational Complexity. This comprehensive methodology enhances the study by providing a comprehensive understanding of the algorithms' performance across various facets, thereby offering a fresh perspective that can facilitate more informed decision-making when selecting image compression techniques.

Practical Implications for Decision-Making:

A salient feature of this paper is its delivery of practical insights and guidance that cater to decision-makers responsible for choosing an image compression method that aligns with their distinct needs. This practical orientation, focused on considerations like image quality preservation and available computational resources, adds immediate value to real-world applications and represents a novel contribution that aids in the translation of research into actionable outcomes.

Detailed Methodology and Implementation:

The study distinguishes itself by providing a clear and precise technique for evaluating the performance of compression methods. This rigorous approach, along with a clear and unified implementation strategy, is an excellent resource for academics and practitioners undertaking similar studies. This sharing of strategy and implementation details is a novel contribution that will stimulate discovery in the subject under consideration.

Relevance to Modern Technology and Communication:

The study underlines the importance of image compression in current technology and communication in recognition of ongoing technical breakthroughs and the increasing demands placed on communication networks and image storage. This acknowledgement of the field's present relevance and importance in tackling current technological concerns is a relevant and interesting contribution.

In summary, the research paper's novelty lies in its systematic comparative analysis of lossless image compression algorithms, its direct response to the practical need for efficient image compression, its incorporation of a diverse range of performance metrics, its provision of practical decision-making insights, its detailed methodology and implementation sharing, and its recognition of the field's relevance to modern technology and communication. Collectively, these distinctive contributions serve to augment the significance of this research in the realm of image compression and its practical applications in the domains of science and technology.

Lossless Image Compression Algorithms Overview:

As technology continues to advance, the demands on communication networks have grown. However, with the increasing gray level resolution and pixel size in sensor and digital image technology, the greater bandwidth does not meet the needs. This is where image compression steps in as a significant field of research. Image compression [11] contributes by reducing the number of bits needed to represent an image, all the while preserving the image's original quality. In basic terms, this process can be likened to reducing the dimensions of a sizable puzzle piece while preserving all critical components and details intact. Figure 1 represents a general concept of image compression.

Figure 1: Image Compression Procedure [12].

Figure 2: Images Obtained through the Utilization of Lossless Compression Technique [13]

Over time, various methodologies have been devised to compress images, primarily categorized into two groups: those altering image quality slightly (lossy compression), and those maintaining original quality (lossless compression) [14]. This research paper delves into these techniques to facilitate efficient image storage and swift transmission.

Lossy compression works by consistently removing redundant information from a file. However, only a portion of the original data remains when the file is uncompressed. This method is commonly applied to situations where slight data loss is not easily noticed by users, such as in video and audio files. On the web, JPEG compression is often used for images. Lossy compression [15] gives smaller images, but it does come with a little loss of quality. It is the preferred choice among users, as it effectively manages to achieve an optimal trade-off between compression efficiency and the preservation of high-quality output. Furthermore, these approaches provide notably superior compression ratios in contrast to lossless methods. Lossless compression entails the manipulation of each individual pixel, ensuring that all the original data bits remain unaltered even after file decompression. This process leads to the reconstruction of images identical to the originals, enabling the complete recovery of information. Consequently, this lossless compression technique attains a moderate level of compression [11] [13][16]. Contemplating the concept of lossless image compression is akin to maintaining the image's integrity while reducing its size. Image compression, on the other hand, can be likened to organizing a cluttered room – it involves eliminating unnecessary elements, retaining only the essential components, resulting in a cleaner and more orderly space. In the realm of images, we follow a similar principle. Our objective is to reduce the size of image files by eliminating non-essential elements, thereby conserving space and enhancing their efficiency for internet transmission. Figure 1 is visual representation of an image before and after undergoing lossless compression technique. The performance evaluation of following lossless compression algorithms was conducted in this research paper:

Run-Length Encoding (RLE):

The RLE lossless compression algorithm presents a simple yet effective approach to data compression. While it may not excel in all scenarios, its strengths in terms of simplicity, speed, and data preservation make it a valuable tool in various applications, particularly in resource-constrained environments or situations where data integrity is non-negotiable. RLE is a simple image compression algorithm that replaces consecutive repeated pixels with a single pixel value and a count. This algorithm is effective for images with long sequences of identical pixels[17]. RLE serves as a straightforward and efficient method for reducing image sizes, particularly when dealing with binary images. However, there is a caveat to consider: in some instances, it may actually increase the size of an image, which presents an issue. This technique preserves all data without loss. Rather than concentrating on intricate patterns, it assesses data repetition frequency as its core approach [12].

Differential Pulse Code Modulation (DPCM):

DPCM is a powerful and widely utilized lossless image compression algorithm, wellsuited for applications that demand pixel-perfect preservation of image data. DPCM achieves efficient compression and data fidelity preservation by capitalizing on local spatial correlations and adaptively encoding image variances. DPCM [18] helps us improve the quality of the signal to get better compression without sacrificing image quality. Within DPCM, a prediction filter is employed to minimize quantization errors. This enhancement not only enhances the Signal-toNoise Ratio (SNR) but also facilitates more effective noise filtering using less bandwidth [19]. DPCM [20] stands out as a key player in spatial domain methods for image compression. Its innovative approach addresses predictive coding constraints, leading to fewer residues and achieving higher compression ratios.

Burrows-Wheeler Transform (BWT):

The BWT is a potent lossless compression algorithm with a particular knack for image data. By reorganizing data to expose redundancy and employing a non-adaptive transformation, BWT achieves remarkable compression ratios while preserving data integrity. BWT rearrange [21] the image data in a smart way by encoding the difference between the original data and the transformed data. This encoding is done in a way that is very efficient and makes the file smaller. The BWT is fully reversible and minimally impacts data storage, requiring only a small amount of extra space for the last character's position. This transformed sequence can be efficiently compressed using run-length coding. Detailed instructions for both forward and reverse BWT are available in reference [22]. BWT method [23] combines the ideas of encryption and compression to make data both smaller and safer. During the evaluation, it was determined that the BWT method reduced the data size to nearly 90% of its original size. Additionally, it excels in safeguarding the secrecy of the original data and the associated encryption key [24] It not only significantly reduces the size of the images but also guarantees that they maintain a high level of visual sharpness and quality. BWT [25] is like rearranging pieces of a puzzle by predicting what symbols come next in the image using something called context mixing.

Material and Method

In this section, we presented a detailed approach to comparing three image compression methods – RLE, BWT and DPCM – while maintaining image quality. Our methodology encompasses data collection, algorithm implementation, measurement criteria selection, and experimentation.

Data Collection:

To evaluate the effectiveness of image compression techniques we collected a range of images that encompassed subjects and scenarios [26]. Our image selection process was methodical, taking into careful consideration factors such as image dimensions, chromatic diversity, and the degree of intricacy. Our dataset comprises images of sizes ranging from 256x256, to 1024x1024 pixels. These selected images also encompass diverse levels of intricacy and utilize both 8-bit and 24-bit color schemes. This broad spectrum of detail serves to enable a comprehensive evaluation of how effectively the algorithms function in response to color precision demands.

Moreover, our dataset comprises color styles of images including grayscale images, with one intensity channel and RGB images with red, green, and blue channels. By including this set of images, we can evaluate the performance of the selected image compression techniques across a wide array of real-world scenarios. This approach provides us with insights into how these algorithms deal with image characteristics and complexities aiding us in our analysis.

Evaluation Metric:

We evaluated the algorithms using key metrics, which include Peak Signal-to-Noise Ratio (PSNR), Bit Rate, Mean Squared Error (MSE), Structural Similarity Index (SSIM), and Computational Complexity. Bit Rate quantifies the average number of bits needed to represent each pixel in the compressed image. It holds significant importance in assessing storage space and transmission bandwidth requirements. Lower bit rates signify more efficient compression, leading to reduced memory usage and faster data transmission. In simpler terms, lower bit rates result in improved compression, making image storage and sharing more practical. The specific range depends on the desired compression level and available bandwidth. The optimal bit rate is contingent on the acceptable balance between image quality and file size, a criterion that varies according to the application and individual user preferences. In high-quality applications, one might opt for a higher bit rate to ensure the preservation of image fidelity. In bandwidthconstrained or streaming scenarios, lower bit rates are preferred to reduce data transmission requirements. The specific range for bit rate will vary based on your application's requirements [27][28][29][30][31]. Computational Complexity evaluates the computational resources required for the compression process. It measures the time and processing power needed to execute the algorithm. Lower computational complexity is preferable, as it ensures faster compression and decompression, making the algorithm suitable for real-time applications and resourceconstrained devices. Lower computational complexity is desirable for real-time or resourceconstrained applications. The range for computational complexity depends on the available hardware and real-time processing requirements. There is no specific numerical range for computational complexity, but it should be kept as low as possible while meeting the application's performance needs. The optimum range for computational complexity depends on the available hardware and the specific requirements of the application [32][33][34][35][36]. MSE quantifies the average squared difference between the compressed and original images. A lower MSE value signifies better preservation of image quality. However, MSE may not accurately represent perceived image quality, as it treats all pixel errors equally and is sensitive to outliers. Typically, MSE ranges from 0 to positive infinity. Lower MSE values indicate better image quality. The optimum range for MSE depends on the desired image quality. If extremely high image quality is required, MSE will be as low as possible, approaching zero. However, in some cases, a slightly higher MSE may be acceptable if it results in significantly smaller file sizes or faster compression [37][38][39][40][41]. PSNR is a widely used metric that measures the ratio of the maximum possible pixel intensity to the MSE. It gauges the fidelity of the compressed image with respect to the original. Higher PSNR values indicate superior image quality, as the compressed image closely approximates the original image. Typically, PSNR ranges from 0 to 60. PSNR value above 30 is considered good for most applications. For high-quality applications like medical imaging or archival storage, a PSNR value above 40 might be desired [42][43][44][45][46]. SSIM measures the structural similarity between the compressed and original images, considering luminance, contrast, and structure. Unlike MSE and PSNR, SSIM reflects the perceived image quality, making it more aligned with human perception. Higher SSIM values correspond to better compression performance, as the compressed image preserves more perceptual details. SSIM values range from -1 to 1, with 1 indicating perfect similarity. A value above 0.9 is considered good for image quality. SSIM is preferred when you want to measure perceptual image quality, as it considers structural information in addition to pixel value [47][48][49][50][51]. PSNR and SSIM measure image quality, while MSE represent image similarity. Compression ratio is calculated based on the ratio of original image size to compressed size, and computational complexity is proportional to image size. The algorithms are evaluated on five test images. The average evaluation results across all images are computed for each algorithm. The resulting performance metrics are compared and visualized through bar plots to enable a comprehensive analysis of the image compression techniques.

Implementation:

The implementation of the image compression comparison involves clear, concise, and coherent steps to evaluate algorithms and assess their performance as shown in Figure 3. The main objective of this study is to compress images and analyze various metrics. The initial step involves data collection, wherein data is gathered and provided as input to the code. The process commences by initializing the environment and input parameters, which include image filenames and the desired compression ratio. Subsequently, we proceed to read the image and assess whether it requires conversion to grayscale. Next, we implemented three compression techniques in a manner; RLE is used to compress the image data followed by applying the BWT to transform the data and finally utilizing DPCM for encoding the pixels. Lastly, we evaluated performance metrics such as PSNR, SSIM, MSE, RMSE and compression ratio to assess the quality of the resulting image. Furthermore, we meticulously documented essential factors such as bitrate and computational complexity to ensure the depth of our analysis. Subsequently, we compute averages across all images and generate visual comparisons for each algorithm.

Figure 3: Implementation of the image compression comparison

Results and Analysis

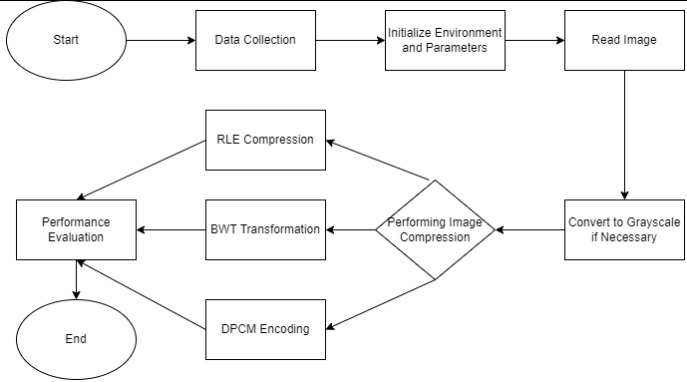
Our experiments unveiled the performance of RLE, DPCM, and BWT through the application of diverse metrics. PSNR and SSIM scores provided insights into the preservation of image quality, where higher scores indicated superior performance. Lower MSE values denoted fewer errors, which is a favorable outcome. Bitrate offered insights into the compression levels, while computational complexity shed light on the algorithms' efficiency in utilizing processing time and resources. These measurements furnish a clear and direct means of evaluating the effectiveness of the algorithms.

Figure 4: PSNR comparison graph

Figure 5: SSIM comparison graph

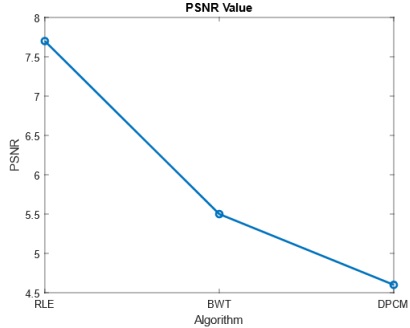
The PSNR chart (in Figure 4) is a useful tool for evaluating lossless image compression algorithms. The y-axis measures PSNR values, quantifying compressed image quality, while the x-axis lists the algorithms under examination. RLE achieves an impressive PSNR of 7.7, indicating excellent image quality preservation and effective compression. Following closely, BWT achieves a PSNR of 5.5, indicating slightly lower image quality than RLE but still offering reasonable compression without significant detail loss. DPCM records the lowest PSNR at 4.6, suggesting it introduces more noticeable artifacts and compromises image quality. In summary, RLE excels with the highest image quality, making it suitable for applications prioritizing image fidelity. BWT, while slightly lower in PSNR compared to RLE, maintains acceptable image quality and is suitable when balancing compression and quality is important. DPCM, with the lowest PSNR, should be chosen carefully, especially in applications where preserving image quality is paramount.

The SSIM comparison chart (Figure 5) offers crucial insights into the performance of various lossless image compression algorithms. On this graph, the y-axis represents SSIM values, which measure the structural similarity between the original and compressed images. Meanwhile, the x-axis lists the algorithms being assessed. RLE obtains the lowest SSIM value among the algorithms at 0.005. This signifies a substantial structural dissimilarity between the compressed and original images when using RLE, indicating a significant loss of image fidelity. When we consider SSIM, we observe that BWT outperforms RLE with a score of 0.3, indicating a higher degree of structural similarity, though not an exact match to the original image. DPCM also achieves a score of 0.29, which is close to BWT, suggesting comparable structural likeness but still some variance from the original. In summary, BWT attains the highest SSIM score, indicating that it preserves structural details better than RLE and DPCM. However, it is crucial to acknowledge that even with BWT and DPCM, there remains a significant structural difference from the original image. This underscores the challenge of retaining fine structural details in lossless compression techniques.

Figure 6: MSE comparison graph

Figure 7: Bitrate comparison graph

When we delve into the MSE comparison chart (Figure 6), it proves to be a robust tool for assessing different lossless image compression methods. The y-axis displays MSE values, representing the average squared difference between original and compressed images, while the x-axis identifies the algorithms under scrutiny. RLE shows the lowest MSE value among the algorithms, scoring 1.5 x 104. This indicates minimal distortion between the compressed and original images when using RLE, making it excel in preserving image quality compared to the others. BWT follows RLE with an MSE of 1.85 x 104, suggesting slightly higher distortion but still within an acceptable range for maintaining image quality. DPCM records the highest MSE value among the algorithms, at 2.55 x 104. This signifies greater distortion when using DPCM for compression, implying a lower image quality after compression compared to RLE and BWT. In summary, RLE stands out as the best performer in minimizing image distortion, boasting the lowest MSE value. BWT closely follows, introducing slightly more distortion but still preserving image quality well. On the other hand, DPCM introduces a higher degree of distortion, indicating comparatively lower image quality post-compression.

The bit rate comparison chart (in Figure 7) is a valuable tool for assessing various lossless image compression algorithms. On this chart, the y-axis measures bit rate in bytes, while the xaxis lists the algorithms under consideration. RLE displays a bit rate of 1.12 bytes, indicating it requires slightly more storage space, on average, to represent compressed images. While still effective, this higher bit rate suggests it may not achieve compression levels as impressive as some other algorithms. However, BWT shines with a 1-byte Bit Rate, highlighting superior compression efficiency compared to RLE. This suggests that BWT can offer better compression ratios while preserving image quality. Similarly, DPCM also achieves a 1-byte Bit Rate, demonstrating efficient compression with minimal storage requirements. Both BWT and DPCM excel in terms of bit rate, demanding minimal storage space for compressed images.

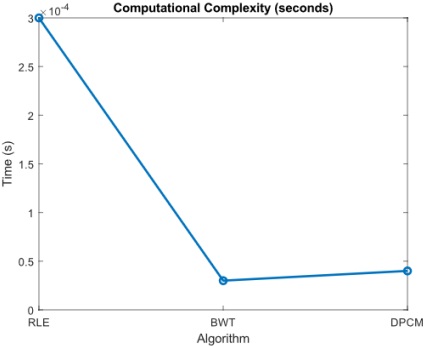
Figure 8: Computational complexity comparison graph

Now, turning to the computational complexity comparison chart (in Figure 8), it becomes a valuable tool for evaluating the efficiency of various lossless image compression algorithms. The y-axis quantifies computational complexity in seconds or related units, while the x-axis lists the algorithms under examination. RLE stands out as a top performer with a low computational complexity of 3 x 10-4 seconds, highlighting its efficiency in swiftly compressing or decompressing images, making it an excellent choice for scenarios with limited computational resources, even though it may not achieve the highest compression ratios. BWT closely follows with a slightly higher computational complexity of 0.3 x 10-4 seconds. While it demands a bit more computational effort than RLE, this trade-off is justified by the improved compression ratios it offers. DPCM presents a computational complexity of 0.4 x 10-4 seconds, slightly higher than both RLE and BWT. Much like the BWT, DPCM achieves a harmonious equilibrium between computational requirements and compression efficiency, presenting a beneficial compromise that optimizes resource utilization while maintaining compression performance. In summary, RLE emerges as the most computationally efficient algorithm, making it well-suited for scenarios with strict computational constraints, even though it may not achieve the highest compression ratios. BWT and DPCM, while slightly more computationally demanding, provide improved compression efficiency

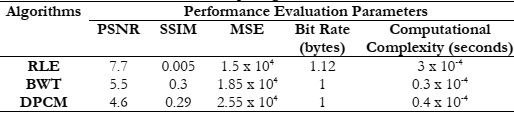
Table 1: Consolidated table comprising values of RLE, BWT and DPCM

Table 1 shows the consolidated table comprising values of RLE, BWT and DPCM. The RLE algorithm exhibits moderate PSNR, indicating a reasonable level of image quality preservation. However, its SSIM score is low, suggesting poor structural similarity. The MSE value is high, implying a substantial error in pixel value prediction. On the positive side, RLE achieves a low bit rate, making it efficient in terms of compression. Its computational complexity is also notably low, making it suitable for real-time applications.

The BWT algorithm offers a lower PSNR compared to RLE, indicating a degradation in image quality. However, it exhibits a higher SSIM score, suggesting better structural similarity. The MSE value remains high, signifying pixel value prediction errors. BWT excels in terms of bit rate, achieving a highly efficient compression. The computational complexity is low, making it suitable for applications with modest time constraints. Among the three algorithms, DPCM records the lowest PSNR, signaling a notable decline in image quality. The low SSIM score indicates suboptimal structural similarity, and the highest MSE value underscores substantial errors in pixel prediction. Similar to BWT, DPCM attains an efficient bit rate. Its computational complexity is reasonable, albeit slightly higher than that of BWT.

Conclusion

This research conducted a thorough examination of three crucial lossless image compression methods: RLE, BWT, and DPCM. Employing a systematic analysis that incorporated metrics such as PSNR, SSIM, MSE, RMSE, Bitrate, and Computational Complexity, the study elucidated the merits and limitations of each algorithm. RLE, acknowledged for its simplicity and capacity to preserve data, demonstrates proficiency in upholding image quality but might not consistently attain the most aggressive compression ratios. BWT, with its remarkable compression efficiency, offers a competitive balance between compression ratios and image quality. DPCM, while maintaining image quality well, provides a compromise between resource-efficient compression and image fidelity. Selecting the most appropriate algorithm can be a complex decision, particularly when specific application requirements are not readily available. In such cases, the BWT emerges as a favorable choice. BWT offers a harmonious blend of compression efficiency and image quality preservation, making it a versatile solution for a wide range of image compression applications. Nevertheless, it is crucial to reiterate that the ultimate decision should be based on a comprehensive evaluation of the unique demands and limitations of your specific application.

Reference

[1] M. A. Rahman, M. Hamada, and M. A. Rahman, “A comparative analysis of the state-ofthe-art lossless image compression techniques,” SHS Web Conf., vol. 139, p. 03001, 2022, doi: 10.1051/SHSCONF/202213903001.

[2] N. A. N. Azman, S. Ali, R. A. Rashid, F. A. Saparudin, and M. A. Sarijari, “A hybrid predictive technique for lossless image compression,” Bull. Electr. Eng. Informatics, vol. 8, no. 4, pp. 1289–1296, Dec. 2019, doi: 10.11591/EEI.V8I4.1612.

[3] R. Naveen Kumar, B. N. Jagadale, and J. S. Bhat, “A lossless image compression algorithm using wavelets and fractional Fourier transform,” SN Appl. Sci., vol. 1, no. 3, pp. 1–8, Mar. 2019, doi: 10.1007/S42452-019-0276-Z/FIGURES/8.

[4] M. A. Rahman, M. Hamada, and J. Shin, “The Impact of State-of-the-Art Techniques for Lossless Still Image Compression,” Electron. 2021, Vol. 10, Page 360, vol. 10, no. 3, p. 360, Feb. 2021, doi: 10.3390/ELECTRONICS10030360.

[5] M. A. Rahman and M. Hamada, “PCBMS: A Model to Select an Optimal Lossless Image Compression Technique,” IEEE Access, vol. 9, pp. 167426–167433, 2021, doi: 10.1109/ACCESS.2021.3137345.

[6] H. Zhang, F. Cricri, H. R. Tavakoli, N. Zou, E. Aksu, and M. M. Hannuksela, “Lossless Image Compression Using a Multi-scale Progressive Statistical Model,” Lect. Notes Comput. Sci. (including Subser. Lect. Notes Artif. Intell. Lect. Notes Bioinformatics), vol. 12624 LNCS, pp. 609–622, 2021, doi: 10.1007/978-3-030-69535-4_37/COVER.

[7] R. Suresh Kumar and P. Manimegalai, “Near lossless image compression using parallel fractal texture identification,” Biomed. Signal Process. Control, vol. 58, p. 101862, Apr.2020, doi: 10.1016/J.BSPC.2020.101862.

[8] M. Otair, L. Abualigah, and M. K. Qawaqzeh, “Improved near-lossless technique using the Huffman coding for enhancing the quality of image compression,” Multimed. Tools Appl., vol. 81, no. 20, pp. 28509–28529, Aug. 2022, doi: 10.1007/S11042-022-12846- 8/METRICS.

[9] M. A. Rahman and M. Hamada, “A prediction-based lossless image compression procedure using dimension reduction and Huffman coding,” Multimed. Tools Appl., vol. 82, no. 3, pp. 4081–4105, Jan. 2023, doi: 10.1007/S11042-022-13283-3/METRICS.

[10] M. A. Rahman and M. Hamada, “A Semi-lossless image compression procedure using a lossless mode of jpeg,” Proc. - 2019 IEEE 13th Int. Symp. Embed. Multicore/Many-Core Syst. MCSoC 2019, pp. 143–148, Oct. 2019, doi: 10.1109/MCSOC.2019.00028.

[11] S. C. Satapathy, V. Bhateja, M. Ramakrishna Murty, N. Gia Nhu, and Jayasri Kotti, Eds., “Communication Software and Networks,” vol. 134, 2021, doi: 10.1007/978-981- 15-5397-4.

[12] M. A. Rahman and M. Hamada, “Lossless Image Compression Techniques: A State-ofthe-Art Survey,” Symmetry 2019, Vol. 11, Page 1274, vol. 11, no. 10, p. 1274, Oct. 2019, doi: 10.3390/SYM11101274.

[13] M. A. Al-jawaherry and S. Y. Hamid, “Image Compression Techniques: Literature Review,” J. Al-Qadisiyah Comput. Sci. Math., vol. 13, no. 4, p. Page 10-21-Page 10 – 21, Dec. 2021, doi: 10.29304/JQCM.2021.13.4.860.

[14] L. S. S. P. Amandeep Kaur, Sonali Gupta, “COMPREHENSIVE STUDY OF IMAGE COMPRESSION TECHNIQUES,” J. Crit. Rev, vol. 7, no. 17, pp. 2382–2388, 2020.

[15] Y. L. Prasanna, Y. Tarakaram, Y. Mounika, and R. Subramani, “Comparison of Different Lossy Image Compression Techniques,” Proc. 2021 IEEE Int. Conf. Innov. Comput. Intell. Commun. Smart Electr. Syst. ICSES 2021, 2021, doi: 10.1109/ICSES52305.2021.9633800.

[16] A. K. Singh, S. Bhushan, and S. Vij, “A Brief Analysis and Comparison of DCT- and DWT-Based Image Compression Techniques,” pp. 45–55, 2021, doi: 10.1007/978-981- 15-4936-6_5.

[17] A. Birajdar, H. Agarwal, M. Bolia, and V. Gupte, “Image Compression using Run Length Encoding and its Optimisation,” 2019 Glob. Conf. Adv. Technol. GCAT 2019, Oct. 2019, doi: 10.1109/GCAT47503.2019.8978464.

[18] K. L. Precious, G.B. and Giok, “A COMPARATIVE ANALYSIS OF IMAGE COMPRESSION USING PCM AND DPCM,” Inf. Technol., vol. 4, no. 1, pp. 60–67, 2020.

[19] G. A. Haidar, R. Achkar, and H. Dourgham, “A comparative simulation study of the real effect of PCM, DM and DPCM systems on audio and image modulation,” 2016 IEEE Int. Multidiscip. Conf. Eng. Technol. IMCET 2016, pp. 144–149, Dec. 2016, doi: 10.1109/IMCET.2016.7777442.

[20] Z. H. Abeda and G. K. AL-Khafaji, “Pixel Based Techniques for Gray Image Compression: A review,” J. Al-Qadisiyah Comput. Sci. Math., vol. 14, no. 2, p. Page 59-70, Jul. 2022, doi: 10.29304/JQCM.2022.14.2.967.

[21] A. Shalayiding, Z. Arnavut, B. Koc, and H. Kocak, “Burrows-Wheeler Transformation for Medical Image Compression,” 11th Annu. IEEE Inf. Technol. Electron. Mob. Commun. Conf. IEMCON 2020, pp. 723–727, Nov. 2020, doi: 10.1109/IEMCON51383.2020.9284917.

[22] “Burrows Wheeler transform - Wikipedia.” Accessed: Nov. 06, 2023. [Online]. Available: https://en.wikipedia.org/wiki/Burrows_Wheeler_transform

[23] M. B. Begum, N. Deepa, M. Uddin, R. Kaluri, M. Abdelhaq, and R. Alsaqour, “An efficient and secure compression technique for data protection using burrows-wheeler transform algorithm,” Heliyon, vol. 9, no. 6, Jun. 2023, doi: 10.1016/j.heliyon.2023.e17602.

[24] G. Devika, R. Sandha, S. Shaik Parveen, and P. Hemavathy, “BURROWS WHEELER TRANSFORM FOR SATELLITE IMAGE COMPRESSION USING WHALE OPTIMIZATION ALGORITHM,” Adv. Appl. Math. Sci., vol. 20, no. 11, pp. 2627– 2634, 2021.

[25] Č. Livada, T. Horvat, and A. Baumgartner, “Novel Block Sorting and Symbol Prediction Algorithm for PDE-Based Lossless Image Compression: A Comparative Study with JPEG and JPEG 2000,” Appl. Sci. 2023, Vol. 13, Page 3152, vol. 13, no. 5, p. 3152, Feb. 2023, doi: 10.3390/APP13053152.

[26] “SIPI Image Database - Misc.” Accessed: Nov. 06, 2023. [Online]. Available: https://sipi.usc.edu/database/database.php?volume=misc

[27] H. Choi and I. V. Bajic, “Scalable Image Coding for Humans and Machines,” IEEE Trans. Image Process., vol. 31, pp. 2739–2754, 2022, doi: 10.1109/TIP.2022.3160602.

[28] N. Le, H. Zhang, F. Cricri, R. Ghaznavi-Youvalari, H. R. Tavakoli, and E. Rahtu, “LEARNED IMAGE CODING FOR MACHINES: A CONTENT-ADAPTIVE APPROACH,” Proc. - IEEE Int. Conf. Multimed. Expo, 2021, doi: 10.1109/ICME51207.2021.9428224.

[29] T. Chen, H. Liu, Z. Ma, Q. Shen, X. Cao, and Y. Wang, “End-to-End Learnt Image Compression via Non-Local Attention Optimization and Improved Context Modeling,” IEEE Trans. Image Process., vol. 30, pp. 3179–3191, 2021, doi: 10.1109/TIP.2021.3058615.

[30] F. Yuan, L. Zhan, P. Pan, and E. Cheng, “Low bit-rate compression of underwater image based on human visual system,” Signal Process. Image Commun., vol. 91, p. 116082, Feb. 2021, doi: 10.1016/J.IMAGE.2020.116082.

[31] S. Cho et al., “Low Bit-rate Image Compression based on Post-processing with Grouped Residual Dense Network”.

[32] A. Lin, B. Chen, J. Xu, Z. Zhang, G. Lu, and D. Zhang, “DS-TransUNet: Dual Swin Transformer U-Net for Medical Image Segmentation,” IEEE Trans. Instrum. Meas., vol. 71, 2022, doi: 10.1109/TIM.2022.3178991.

[33] W. Wang, C. Chen, M. Ding, H. Yu, S. Zha, and J. Li, “TransBTS: Multimodal Brain Tumor Segmentation Using Transformer,” Lect. Notes Comput. Sci. (including Subser. Lect. Notes Artif. Intell. Lect. Notes Bioinformatics), vol. 12901 LNCS, pp. 109–119, 2021, doi: 10.1007/978-3-030-87193-2_11/COVER.

[34] S. W. Zamir, A. Arora, S. Khan, M. Hayat, F. S. Khan, and M. H. Yang, “Restormer: Efficient Transformer for High-Resolution Image Restoration,” Proc. IEEE Comput. Soc. Conf. Comput. Vis. Pattern Recognit., vol. 2022-June, pp. 5718–5729, 2022, doi: 10.1109/CVPR52688.2022.00564.

[35] A. Hatamizadeh et al., “UNETR: Transformers for 3D Medical Image Segmentation,” Proc. - 2022 IEEE/CVF Winter Conf. Appl. Comput. Vision, WACV 2022, pp. 1748– 1758, 2022, doi: 10.1109/WACV51458.2022.00181.

[36] J. M. J. Valanarasu, P. Oza, I. Hacihaliloglu, and V. M. Patel, “Medical Transformer: Gated Axial-Attention for Medical Image Segmentation,” Lect. Notes Comput. Sci. (including Subser. Lect. Notes Artif. Intell. Lect. Notes Bioinformatics), vol. 12901 LNCS, pp. 36–46, 2021, doi: 10.1007/978-3-030-87193-2_4/COVER.

[37] D. Chicco, M. J. Warrens, and G. Jurman, “The coefficient of determination R-squared is more informative than SMAPE, MAE, MAPE, MSE and RMSE in regression analysis evaluation,” PeerJ Comput. Sci., vol. 7, pp. 1–24, Jul. 2021, doi: 10.7717/PEERJ CS.623/SUPP-1.

[38] H. Singh, A. S. Ahmed, F. Melandsø, and A. Habib, “Ultrasonic image denoising using machine learning in point contact excitation and detection method,” Ultrasonics, vol. 127, p. 106834, Jan. 2023, doi: 10.1016/J.ULTRAS.2022.106834.

[39] A. Kumar and M. Dua, “Image encryption using a novel hybrid chaotic map and dynamic permutation−diffusion,” Multimed. Tools Appl., pp. 1–24, Sep. 2023, doi: 10.1007/S11042-023-16817-5/METRICS.

[40] Y. Lu, M. Gong, L. Cao, Z. Gan, X. Chai, and A. Li, “Exploiting 3D fractal cube and chaos for effective multi-image compression and encryption,” J. King Saud Univ. - Comput. Inf. Sci., vol. 35, no. 3, pp. 37–58, Mar. 2023, doi: 10.1016/J.JKSUCI.2023.02.004.

[41] O. Rashid, A. Amin, and M. R. Lone, “Performance analysis of DWT families,” Proc. 3rd Int. Conf. Intell. Sustain. Syst. ICISS 2020, pp. 1457–1463, Dec. 2020, doi: 10.1109/ICISS49785.2020.9315960.

[42] U. Sara, M. Akter, M. S. Uddin, U. Sara, M. Akter, and M. S. Uddin, “Image Quality Assessment through FSIM, SSIM, MSE and PSNR—A Comparative Study,” J. Comput. Commun., vol. 7, no. 3, pp. 8–18, Mar. 2019, doi: 10.4236/JCC.2019.73002.

[43] Y. Huang, B. Niu, H. Guan, and S. Zhang, “Enhancing Image Watermarking with Adaptive Embedding Parameter and PSNR Guarantee,” IEEE Trans. Multimed., vol. 21, no. 10, pp. 2447–2460, Oct. 2019, doi: 10.1109/TMM.2019.2907475.

[44] U. Erkan, D. N. H. Thanh, L. M. Hieu, and S. Enginoglu, “An iterative mean filter for image denoising,” IEEE Access, vol. 7, pp. 167847–167859, 2019, doi: 10.1109/ACCESS.2019.2953924.

[45] A. Elhadad, A. Ghareeb, and S. Abbas, “A blind and high-capacity data hiding of DICOM medical images based on fuzzification concepts,” Alexandria Eng. J., vol. 60, no. 2, pp. 2471–2482, Apr. 2021, doi: 10.1016/J.AEJ.2020.12.050.

[46] W. Chen, B. Qi, X. Liu, H. Li, X. Hao, and Y. Peng, “Temperature-Robust Learned Image Recovery for Shallow-Designed Imaging Systems,” Adv. Intell. Syst., vol. 4, no. 10, p. 2200149, Oct. 2022, doi: 10.1002/AISY.202200149.

[47] W. Y. Juan, “Generating Synthesized Computed Tomography (CT) from Magnetic Resonance Imaging Using Cycle-Consistent Generative Adversarial Network for Brain Tumor Radiation Therapy,” Int. J. Radiat. Oncol. Biol. Physics, vol. 111, no. 3, pp. e111– e11, 2021.

[48] D. R. I. M. Setiadi, “PSNR vs SSIM: imperceptibility quality assessment for image steganography,” Multimed. Tools Appl., vol. 80, no. 6, pp. 8423–8444, Mar. 2021, doi: 10.1007/S11042-020-10035-Z/METRICS.

[49] J. Nilsson and T. Akenine-Möller, “Understanding SSIM,” Jun. 2020, Accessed: Nov. 06, 2023. [Online]. Available: https://arxiv.org/abs/2006.13846v2

[50] V. V. Starovoitov, E. E. Eldarova, and K. T. Iskakov, “Comparative analysis of the ssim index and the pearson coefficient as a criterion for image similarity,” Eurasian J. Math. Comput. Appl., vol. 8, no. 1, pp. 76–90, 2020, doi: 10.32523/2306-6172-2020-8-1- 76-90.

[51] J. Peng et al., “Implementation of the structural SIMilarity (SSIM) index as a quantitative evaluation tool for dose distribution error detection,” Med. Phys., vol. 47, no. 4, pp. 1907–1919, Apr. 2020, doi: 10.1002/MP.14010.

Research Article

International Journal of Innovations in Science & Technology