E-ISSN:2709-6130
P-ISSN:2618-1630

Research Article

International Journal of Innovations in Science & Technology

2023 Volume 5 Number 4 Oct-Dec

Numerical Analysis of Flow Past Over Square Rods Using Control Rod at Distinct Gap Spacing

Manzoor. R1, Kalsoom. S2, Naeem. A1, Nadeem. N1, Aziz. G1

1 Mathematics Department, SBK Women’s University Quetta, 44000 Pakistan

2 Mathematics Department, Air University, Islamabad.

Abstract
The influence of Reynolds number and gap spacing on flow via two detachable square rods with a small control rod in between is examined using two-dimensional numerical simulations. The range of gap spacing is determined by taking Re = 80–200 and g = 0.50–6.0. First, the impact of the computational domain and the accuracy of the grid points are analysed. Among these are crucial flow modes, fully formed two rows of vortex shedding flows, fully developed regular and irregular vortex shedding flows, consistent flow, and shear layer reattachment. For every combination of (Re, g), the Cdmean of the C1 rod is higher than the Cdmean of the C2 rod. Additionally, push causes Cdmean2 values to be negative between g = 0.50 and 2.0. The value of Cdmean that is larger is 1.3907 (Re, g) = (150, 3.0). Furthermore, for (Re, g) = (200, 3.0) and (200, 1.50), respectively, for C1 and C2, the greatest percentage decrease in Cdmean is 19.3% and 120.3%, respectively.

Keywords: Reynolds number, Control rods, lattice Boltzmann method, Vortex Shedding, Energy Spectrum, Cdmean.

Corresponding Author How to Cite this Article
Raheela Manzoor, Mathematics Department, SBK Women’s University Quetta, 44000 Pakistan
 Raheela Manzoor, Shazia Kalsoom, Asma Naeem, Noreen Nadeem, Gohar Aziz, Numerical Analysis of Flow Past Over Square Rods Using Control Rod at Distinct Gap Spacing. IJIST. 2023 ;5(4):661-676 https://journal.50sea.com/index.php/IJIST/article/view/561

Introduction

The flow interaction with objects, whether square, rectangular, or circular, has attracted attention in a wide range of engineering fields due to its usefulness in the construction of cooling towers, high-rise buildings, bridges, and micro-electro-mechanical systems. Flow interacts with an object to cause it to vibrate. Consequently, vortex shedding happens, which could damage an object's structure. Therefore, it is essential to control flow using vortex shedding and energy conservation. To reduce fluid force and control flow in this situation, several researchers use the passive control method (PCM), which has been reported in the literature.

The aerodynamic force drop for flow past a detachable circular rod with two control plates placed next to the main circular rod is investigated numerically by [1]. They discovered that vortex shedding near the wake is decreased more when the control plate is positioned in the down position than when it is positioned in the up position. A numerical simulation based on the control plate's impact on the square rod is carried out by [2]. The control plate's length was varied for this research between w = 0.50 and 6.0 at a constant Reynolds number. It was found that the control plate generated a strong hydrodynamic interaction with the wake and strongly restricted vortex shedding in the vicinity of the rod's wake [3]. In order to lessen the fluid force operating on a square rod that is upstream and separated from a thin, flat plate, we conducted a numerical analysis. The distance between the plate and rod can be changed from 1.1 to 7.0 by widening the flat plate from w = 0.10 to 0.90. Re = 50.0–200 is the range of Reynolds numbers that must be employed. They also found the optimal flat plate width and gap spacing at g = 3.0 and w = 0.5, where the greatest decrease in fluid force was seen. Control rods, which are positioned either upstream or downstream to manage flow, are the subject of numerous further studies, much like control plates [4][5][6][7][8][9][10][11][12][13][14].

Two tiny control rods with a diameter of d1 = D/8 next to the main square rod were employed in a numerical study based on the passive control technique by [15]. According to the study, reducing the range of Re led to a reduction in forces of between 70.0% and 80.0%. In an experiment [16], used four tiny control rods spaced from the main circular rod with g = 1.07 and Re = 2400 - 7600 to establish vortex-induced vibration of a deep water riser. The maximum reduction in drag and mitigation of vortex shedding have been noted. A quantitative study of the gap distance between the square rod and control rod at Re = 150 was carried out by [17]. The effect of the control rod decreased as the value of g approached 5.0, they found after distinguishing two distinct flow modes at the critical value of g = 2.3. In order to determine the reduction of forces on the main square rod, [18] carried out a numerical research with a small control rod positioned next to the main square rod at Re = 100. He discovered a drag force reduction of 10.0% to 15.0% [19] uses numerical simulations in two and three dimensions to examine how a control rod affects the fluid force decrease during flow over a circular rod. They found that as the distance between the main rod and control rod increased, the values of the Strouhal number (St) grew discontinuously. In [20], the fluid flow past a circular rod coupled to microscopic control rods was numerically investigated. It was shown that the gap spacing, Reynolds number, and angle of attack all affected the vortex-induced vibration suppression process. investigated how Reynolds numbers affected the flow past a square rod when a control rod was present [11][21]. By applying LBM to statistically analyze flow past a square rod that was connected to control rods [22], found that the maximum reduction in drag occurred for Re = 80 at g = 2.5. According to the previously mentioned literature, flow past two major rods when a small control rod is positioned between the main rods has not received much attention, necessitating cautious attention.

Objective:

The aim of this work is to thoroughly examine the effects of Reynolds number and gap separation on flow via two main rods with a control rod positioned in between. The flow past these rods will be assessed using vorticity contours, time-trace studies of the lift and drag coefficients, the lift coefficient's power spectrum, and forces like the mean drag coefficient and Strouhal number for different combinations of g and Re.

Novelty:

In order to avoid structural damage, the current work tries to decrease fluid forces and hinder vortex shedding. These constructions include cooling devices, micro-electro-mechanical systems, high-rise skyscrapers, and bridges. When these things engage with flow, an object vibrates. Vortex shedding consequently occurs, which has the power to completely destroy an object's structure. Thus, vortex shedding and energy saving are crucial for flow control. For this reason, the current work uses the passive control approach (PCM) to manage the flow and minimize the fluid force.

The structure of the paper is as follows. Based on the numerical approach used to simulate the current issue, Section 2. Section 3 offers an explanation of the boundary conditions and problem formulation. The analysis of grid independence and the impact of the computing domain are covered in Section 4. Sections 5 and 6 describe the results of their investigation into the effects of the Reynolds number and gap spacings on the physical characteristics and aerodynamic forces, and Section 7 presents the conclusions.

Material and Method

Lattice Boltzmann Method:

The lattice Boltzmann method (LBM) is a helpful computational approach to handle flow problems of any complexity. The Navier-Stokes equation's non-linear component can be easily handled with this method [23]. LBM is explicit in nature and has second order accuracy in space and time [24]. The equation of state is often used to compute pressure [25]. A general overview of LBM will be given in this part; readers are referred to the well-known publications of [23][24] and [25] for more in-depth material. The equations of the governing Navier-Stokes are studied in this paper.

The momentum equation is represented by equation (2), while the continuity is represented by equation (1). The following discretized lattice Boltzmann equation can be produced by applying the Chapman Enskog expansion (Chapman and Cowling, 1970) [26]:

Where τ is the stability parameter and h_i is the density function at point x and time t. In Eq. (3), the particles go to their neighbour node during the streaming phase, which is represented by the left side, and collide during the collision step, which is represented by the right side. The relation provides the equilibrium distribution function, h_i^eq:

ξ_i is the weighting coefficient representation. The coefficient of weighting varies throughout the different LBM models. The two-dimensional nine-velocity-particles model used in this work is called D2Q9 (dimension = D + Q = number of particles) (see Figure 1). The weighting coefficients are as follows:

Figure 1: Lattice square structure (D2Q9).

The density (ρ) and the velocity (u) are defined as:

The speed of sound and pressure are calculated as:

The kinematic viscosity is calculated as

Problem Formulation and Boundary Conditions:

Figure 2 schematically depicts the flow past two main rods with a control rod positioned in between; the diameters of the main rods and the control rod are D and d, respectively. The point upstream before the rod is Lu = 8D, while the downstream location after the rod is Ld = 26.5D. The channel has a length of L and a height of H = 10D. The gap spacing can be expressed using the formula g = s/D, where s is the surface-to-surface distance between the main and control rods. It is crucial to keep in mind that in every scenario taken into account in this numerical analysis, the distance between the main and control rods remains constant. Boundary conditions come in several forms that can be utilised for different problems. The uniform inflow velocity, U_∞, is represented by the parabolic velocity profile u = U_∞ (1-〖Y/H)〗^2, v = 0 at the inlet border. At the outlet, the convective boundary condition is used. The no-slip boundary condition (u = v = 0) is applied to the surface of the control and main rods as well as the channel walls [23][24]. Important variables such as lift (Cl), drag (Cd), Strouhal number (St), and Reynolds number (Re) have coefficients that are defined as :

Figure 2: Schematic diagram of flow past over a main rods in presence of control rod in between them.

Table 1: Selected cases for present simulation at Re = 80 - 200.

Grid Independence and Computational Domain Study:

At (Re, g) = (120, 1.0), a computational domain impact study is carried out for a range of values of Lu Ld and H. Table 2 displays the computational results of Cdmean1, Cdmean2, St1 and St2 derived for different circumstances. Additionally displayed are the variations within the outcomes. It is clear that the Cdmean1 and Cdmean2 perform better at Lu = 8.0d, Ld = 30.0d, and H = 10.0d when compared to previous examples. Accurate results are also obtained when the estimated values of St for both rods are combined with Lu = 8.0d, Ld = 30.0d, and H = 10.0d. In the instances Lu = 8.0d, Ld = 35.0d, H = 10.0d and Lu = 8.0d, Ld = 30.0d, H = 12.0d, the simulation will take a long time to finish. Other chosen scenarios, such as Lu = 6d and Ld = 25.0d, require more grid points. Therefore, Lu = 8.0d, Ld = 30.0d, and H = 10.0d are used to obtain all of the numerical results in this work.

The grid independence of the current code is evaluated by measuring grid points at D = 10.0, 16.0, 20.0, and 24.0 along the surface of the main and control rods. Table 3 shows how the results are calculated at g = 1.0 and Re = 120 utilising physical parameters like Cdmean1, Cdmean2, St1, St2, Clrms1, and Clrms2. It is investigated if calculations using 20.0-point grids produce more appropriate and precise results.

Table 2: Domain independence Study at g = 1.0 and Re = 120.

Table 3: Grid Independence study at g = 1.0 and Re = 120.

Result and Discussion

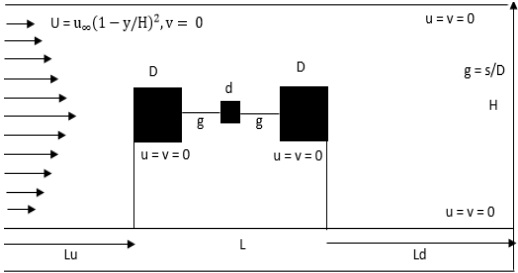
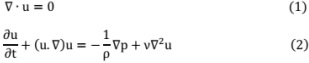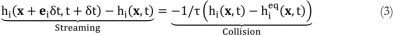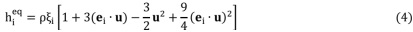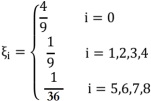A 2-D numerical research is conducted to capture the flow behaviour when a small control rod is positioned between the two main rods. The range of g = 0.50 – 6.0 is used to determine the spacing between the main rods and control rod, while Re is selected between 80 and 200. Based on the analysis, the energy spectrum, vorticity contour, and physical properties are shown.

Vorticity Contour Visualization and Energy Spectrum:

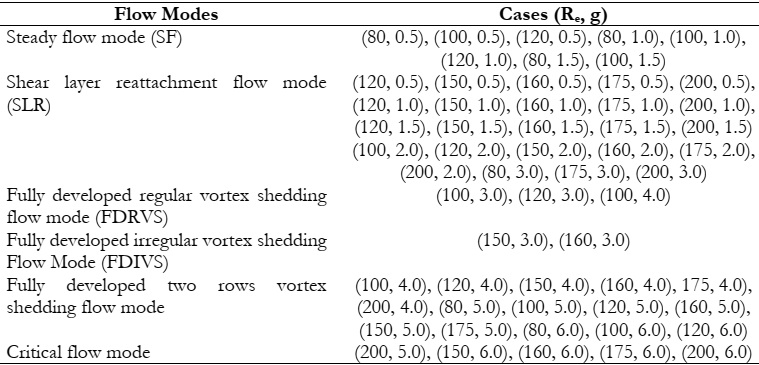
We looked at six different flow modes in the situation of flow past two main rods with a tiny control rod positioned between the main rods at g = 0.50 – 6.0 and Re = 80 – 200 and named them based on their characteristics. At short gap spacings and relatively low Reynolds numbers (g = 0.50 – 1.50 at Re = 80 – 120), the first flow mode is generated. The existence of a control rod has no effect on the fluid flow in this flow mode. Figure 3(a–d) makes it evident how the fluid enters the channel and makes contact with the main rod C1. Without creating any flow between the gaps, the shear layer produced by C1 adhered to the control rod C2 as well as the main rod C2. Moreover, near the rear end of C2, the wake region lengthens as the Reynold number increases (see Figure 3v(a-d)). Vortex shedding did not occur throughout the computational zone as a result. This kind of flow is known as steady flow mode (SFM). There is no difference in lift or drag when vortex shedding is absent. No energy spectrum is produced as a result.

The shear layer detached from C1 in this flow mode and reattached to the in line control rod without creating vortices in the intervals between the breaks. As a result, vortices emerge at the rear end of C2, where the main rod experiences negative vertex shedding at its top surface and positive vortex shedding at its bottom surface. These vortices split off and start moving in different directions after a certain distance. The range of Re determines how many vortices form downstream of the computational domain; the higher the Reynolds number, the more vertices are formed and the shorter the wake zone. Figure 4 (a-c) provides a vivid illustration of this tendency.

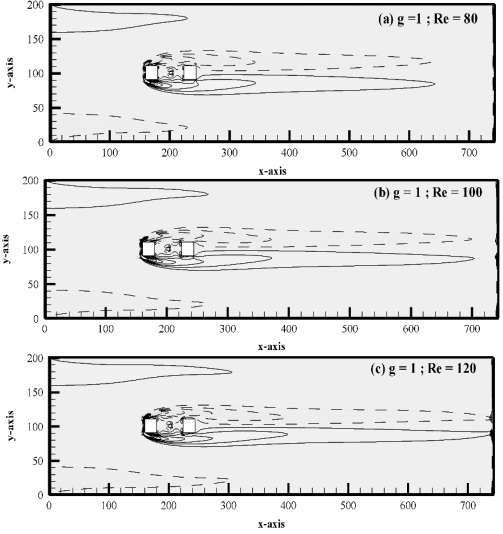
Figure 3: (a-d). Vorticity contour visualization for Steady Flow Mode.

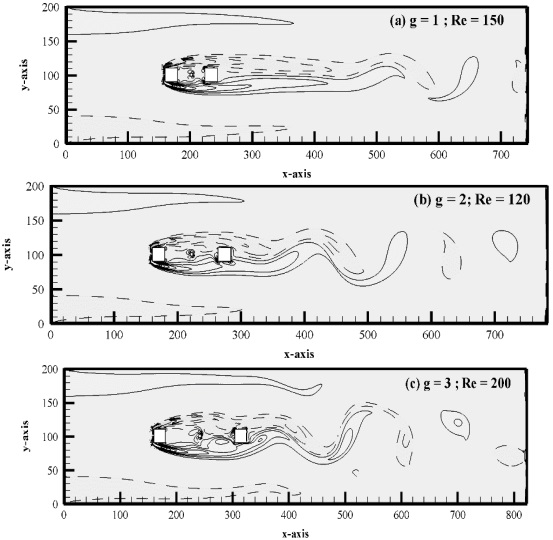
Figure 4: (a-c). Vorticity contour visualization for SLR Flow Mode

For both C1 and C2, the St graph shows a single peak when (Re, g) = (200, 0.50) is taken into account. However, the peak of C2 is broader than the peak of C1 due to a longer wake zone that emerges at C2's downstream location (see Figure 5(a)). However, as Figure 5(e) illustrates, multipeak are occasionally also seen for C2 as a result of both primary and secondary frequency.

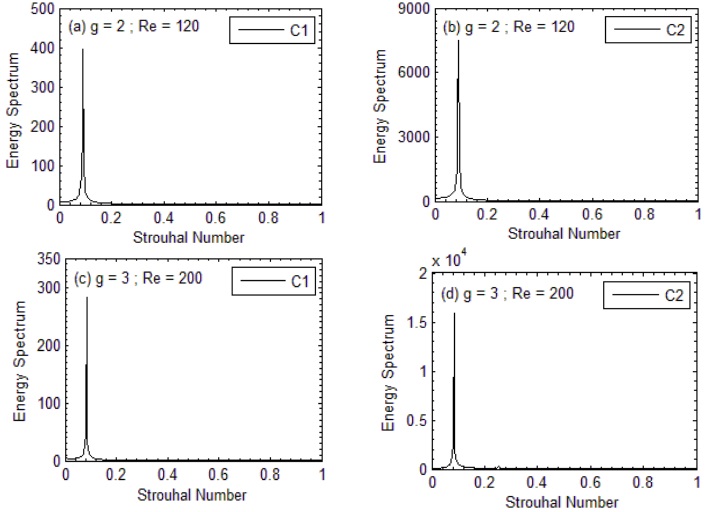
Figure 5: (a-d). Energy Spectrum analysis for SLR Flow Mode.

Currently, there are three flow modes in use: fully developed vortex shedding (FDVS). For Re = 80–160, it is examined at intermediate gap spacing, or g = 3.0 & 4.0. It is clear from Figure 6(a–d) that when there is enough gap separation between the main and control rods, vortices are also formed in the spaces between the gaps caused by the upstream, downstream, and control rods. There are two further classifications for this flow pattern: completely developed regular vortex shedding (i) and fully developed irregular vortex shedding (ii). As demonstrated in Figure 6(a, b), when fully developed normal vortex shedding takes place, vortices form between the gap and the downstream site of C2 and flow regularly towards the computational domain's exit without exhibiting disruptive behaviour. This flow characteristic is found at g = 3.0 and at Re Re = 80–120. Furthermore, behind the C2, a vor-karmann vortex-street forms. However, even if the vortices have fully formed in between the gaps, fully developed irregular vortex shedding shows vortex merging behaviour after reaching downstream of C2. These vortices move irregularly around the computational region. Figure 6(c,d) makes it clear that they are changing in size and strength. This flow mode happens at g = 3.0, at Re = 150 & 160.

C1 only exhibits one peak at (Re, g) = (150, 3.0) and (160, 3.0), but C2 exhibits numerous peaks. When it comes to C2, these various peaks are more noticeable when Re = 160 as opposed to 150. Additionally, it has been noted that when the Reynolds number rises, the value of St decreases.

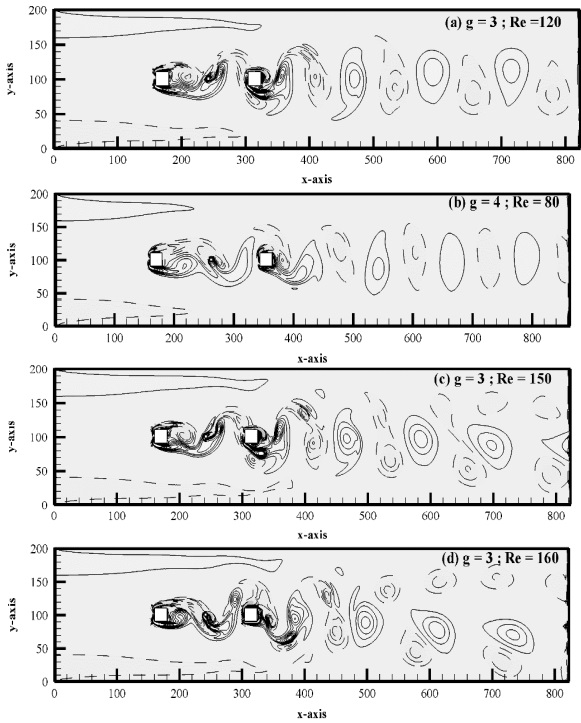
Figure 6: (a-d). Vorticity contour visualization for FDVS flow mode.

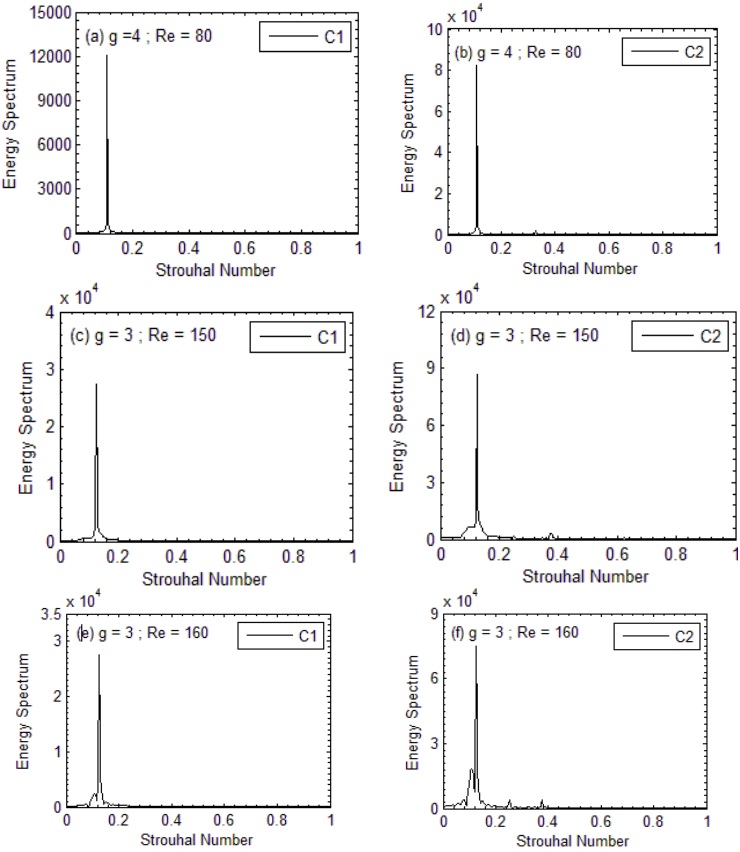
Figure 7: (a-f). Energy Spectrum analysis for FDVS Flow Mode.

An additional flow mode, FDTRVS, is shown in Figure 8(a-d). The vortices completely form within the gaps during this flow phase, however they form two rows downstream of the channel. Instead of moving in opposite directions towards the channel's outlet, positive and negative vortices move in parallel with one another. At Re = 100–200 for g = 4.0, Re = 80–175 for g = 5.0, and Re = 80–120 for g = 6.0, this flow phase was observed. Occasionally, tiny bubbles can be seen above and below the positive and negative vortex rows. It was named this mode. These bubbles cause the fully grown irregular two-row vortex to shed. The suitable energy spectrum, which has a single peak and no multiple peaks, is shown in Figure 9(a-d). For every scenario that was selected, the magnitude of St for C2 is higher than that of C1.

As shown in Figure 10(a, b), critical flow (CF) is seen at gap spacing 5.0 ≤ g ≤ 6.0 and Re from 160 to 200. The vortices in CF combine and deform among themselves after becoming fully developed downstream and within the gaps. The shed vortices are asymmetrical in size and shape and alter in strength as the Reynolds number rises. For every primary rod, the CF mode energy spectrum only reaches a single peak; however, for C2, as shown in Figure 11(a–d), the St peak is wider than it is for C1. All current flow modes for g = 0.50 – 6.0 and Re Re = 80 – 200 are shown in Table 4.

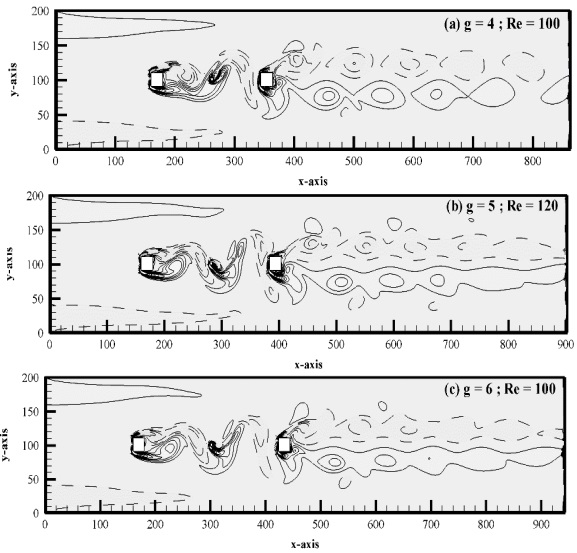
Figure 8: (a-c). Vorticity contour visualization for FDTRVS flow mode.

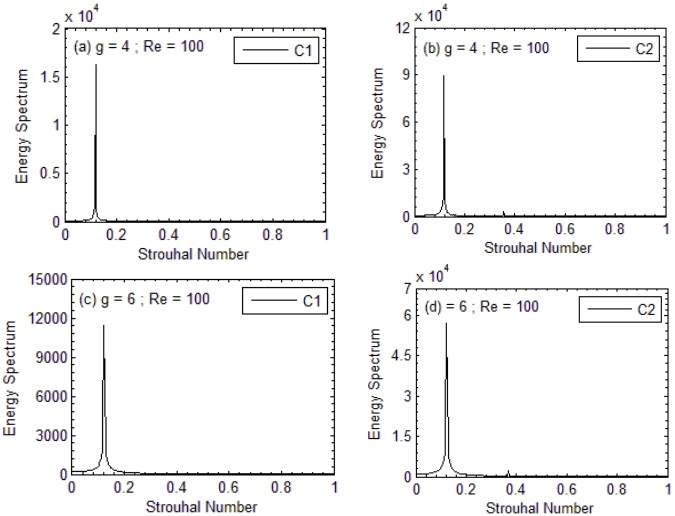
Figure 9: (a-d). Energy spectrum analysis for FDTRVS flow mode.

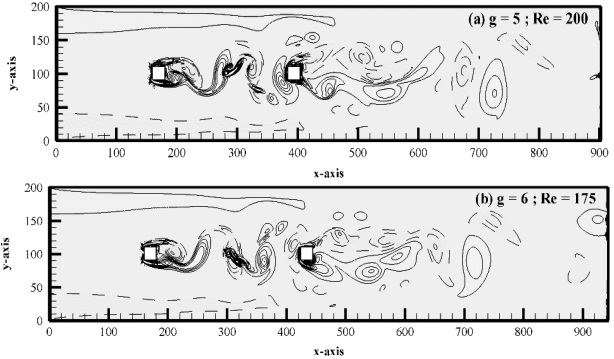
Figure 10: (a-b). Vorticity contour visualization for Critical flow mode.

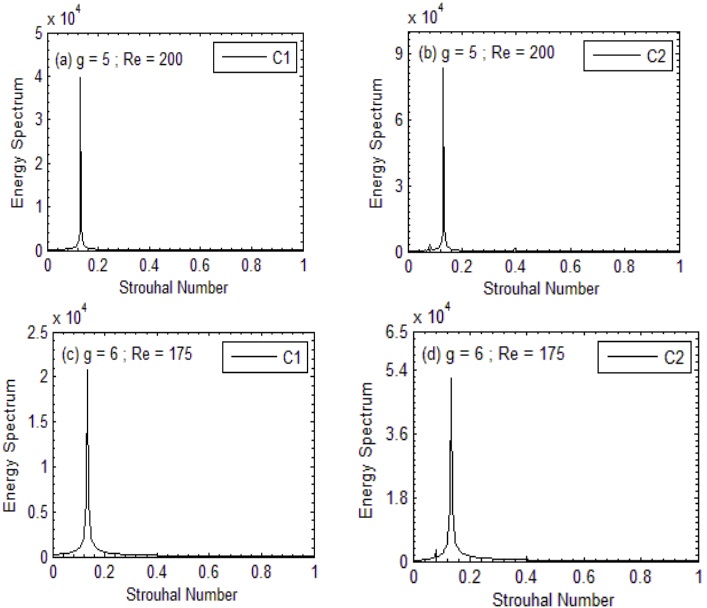
Figure 11: (a-d). Energy Spectrum analysis for Critical flow mode.

Table 4: All existing flow modes at g = 0.50 – 6.0 and Re = 80 – 200.

Effect of Gap Spacing and Reynolds Number on Physical Parameters:

Analyzing specific physical properties, such as Cdmean, Cdrms, Clrms, and St number, can help with the measurement of force fluctuation in fluid structure interaction problems. When g is kept above 3.0, the Cdmean of both rods exhibits increasing and declining behaviors. The SLR flow mode occurred at (Re, g) = (150, 3.0), when the Cdmean of C2 achieved its maximum value of 1.3907. The Cdmean of C2 started to climb at g = 3.0. Its lowest value was also discovered at (Re, g) = (200, 1.0). At (Re, g) = (200, 5.0), or 1.2609, the greatest value of Cdmean was obtained when the current flow mode was Critical (CF).

The drag coefficients (Cdrms) for both rods are displayed as root mean square values in Figure 12(c, d), and they demonstrate both increasing and decreasing behaviour as the Reynolds number rises. For particular Reynolds number values, Cdrms2 was observed to have the biggest magnitude when compared to Cdrms1. The location of the FDTRVS flow mode, (Re, g) = (160, 4), or 0.5168, is where the highest value of Cdrms2 is examined. Despite this, Cdrms1 peaks at (Re, g) = (160, 4.0), or 0.3570. Using the Steady flow SF mode, Cdrms2 and Cdrms1 both reached their lowest value at (Re, g) = (80, 0.5). These are, in order, 0.00003 and 0.00004.

The highest Clrms for C1 are 0.4365 at (Re, g) = (200, 4.0) and the lowest are 0.0000014 at (Re, g) = (80, 1.0). The SLR flow mode is formed at (Re, g) = (150, 3.0), where the maximum value of Clrms for C2 is 1.0303. Moreover, the root mean square values of C1 and C2 are larger than those of a single rod, with the exception of a negligible number of Clrms1 values at Re = 80.

Figure 12(g, h) plots the energy spectrum analysis against Reynolds number. The single rod statistics (g, h) are also shown in Figure 12 for comparison. While the values of St for C1 increase between Re = 80 and 150 before remaining constant for g = 1.0, 1.5, 4.0, and 5.0, the values of St for St1 expand between Re = 80 and 200 for g = 0.5. A mixed pattern is observed for g = 2.0, 3.0, and 6.0 for both C1 and C2, indicating that St1 and St2 behave in an increasing and then decreasing manner initially. In the case of C1, the St is less than the SC. The CF mode occurs at Re = 150–175 for g = 5.0–6.0, and St1 reaches its highest value of 0.1338 at that point. The greatest value of St for C2 is found to be 0.13411 at g = 6.0 and Re = 150–175.

The percentage decline in Cdmean against Re for g = 0.5 – 6.0 is shown in Figure 13(a, b). It begins to rise at g = 0.50 to 2.0, when the percentage reduction increases from Re = 80 to 160; at g = 3.0 to 6.0, it shows a mixed trend with an increase in Re for rod C1. In the case of C2, the mean drag coefficient shows increasing and decreasing behaviour at g = 3.0 and 4.0, but drops from Re = 80 to 200 at g = 0.50 to 2.0 and g = 5.0 & 6.0. At (Re, g) = (200, 3.0), the largest percentage decline in C1 is 19.3%; at (Re, g) = (175, 5.0) and (175, 6.0), the smallest reduction is 2.0. The largest and lowest drops for rod C2 were at (Re, g) = (200, 1.5) and (120, 3.0), at 120.3% and 1.5%, respectively.

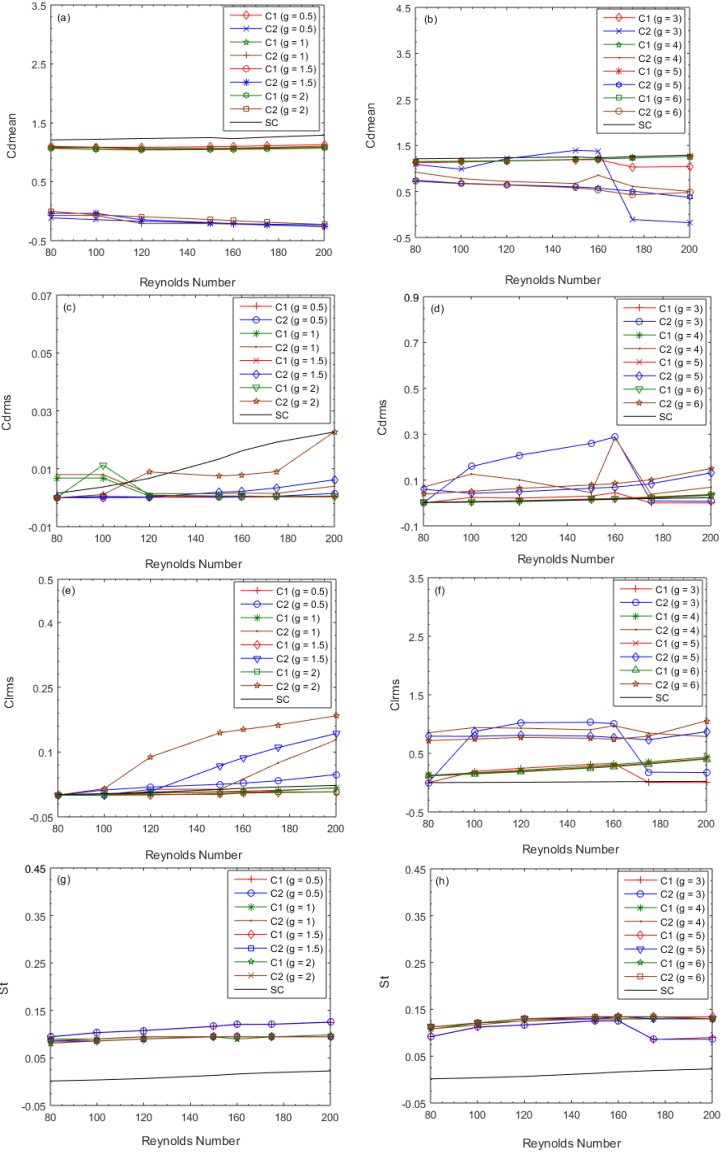
Figure 12: Variation of physical parameters, (a, b) Cdmean, (c, d) Cdrms, (e.f) Clrms and (g, h) St.

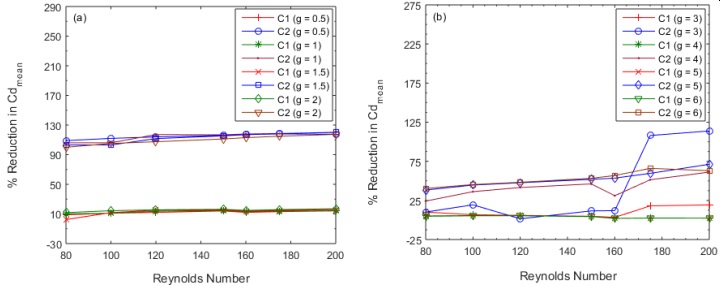
Figure 13: (a, b). Percentage reduction in values of Cdmean.

Conclusion

Examined are the effects of Re and g with Re = 80–200 and g = 0.50–6.0. The following are the primary conclusions of this study:

• The results of this study are utilized to investigate how changes in Re and g result in the acquisition of five distinct flow modes. * The critical flow mode, regular vortex shedding, irregular vortex shedding, two rows vortex shedding, and shear layer reattachment are all completely known flow modes. For any combination of (Re, g), it is noticed that the Cdmean of the C1 rod is bigger than the Cdmean of the C2 rod.Cdmean1 has the largest value at (Re, g) = (200, 5.0), or 1.2609, and Cdmean2 has the maximum value at (Re, g) = (150, 3.0), or 1.3907. * For g = 0.50 – 2.0 at Re = 80 – 200 and g = 3.0 at Re = 170 – 200, the Cdmean for C2 exhibits negative values.

• When the Reynolds number increases from Re = 80 to 200, the Cdrms and Clrms show different patterns.At (Re, g) = (200, 3.0), C1 has the most percentage reduction in Cdmean (19.3%); for C2, the biggest percentage reduction is 120.3% at (Re, g) = (200, 1.5) and (120, 3.0).

• The biggest value of St for C2 is studied at g = 6.0 for Re = 150 – 175, or 0.13411, while the maximum value of St1 is 0.1338 and occurs at Re = 150 – 175 for g = 5.0 – 6.0, while CF mode is occurring.

Nomenclature:

• C1 Upstream rod

• C2 Downstream rod

• Cs Speed of sound

• Cd1 Drag force of upstream rod

• Cd2 Drag force of downstream rod

• Cl1 Lift force of upstream rod

• Cl2 Lift force of downstream rod

• Cdmean1 Mean drag coefficients of upstream rod

• Cdmean2 Mean drag coefficients of downstream rod

• Cdrms Root-mean-square value of drag coefficients

• Clrms Root-mean-square value of lift coefficients

• D Diameter of the rod

• D Diameter of control rods

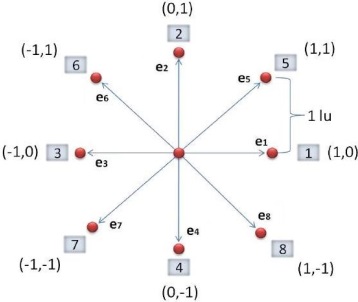
• ei velocity vectors

• Fd Force components in x- directions

• Fl Force components in y- directions

• hi Particle distribution function

• hi(eq) Equilibrium distribution function

• n Number of particles

• p Pressure

• St Strouhal number

• U∞ Uniform inflow velocity

• ξi Weighting coefficient

Reference

[1] J. Y. Hwang and K. S. Yang, “Drag reduction on a circular cylinder using dual detached splitter plates,” J. Wind Eng. Ind. Aerodyn., vol. 95, no. 7, pp. 551–564, Jul. 2007, doi: 10.1016/J.JWEIA.2006.11.003.

[2] C. J. Doolan, “Flat-plate interaction with the near wake of a main rod,” AIAA S. J, vol. 47, pp. 475–478, 2009.

[3] S. Malekzadeh and A. Sohankar, “Reduction of fluid forces and heat transfer on a square cylinder in a laminar flow regime using a control plate,” Int. J. Heat Fluid Flow, vol. 34, pp. 15–27, Apr. 2012, doi: 10.1016/J.IJHEATFLUIDFLOW.2011.12.008.

[4] H. Sakamoto and H. Haniu, “Optimum Suppression of Fluid Forces Acting on a Circular Cylinder,” J. Fluids Eng., vol. 116, no. 2, pp. 221–227, Jun. 1994, doi: 10.1115/1.2910258.

[5] M. A. Z. Hasan and M. O. Budair, “Role of splitter plates in modifying cylinder wake flows,” https://doi.org/10.2514/3.12243, vol. 32, no. 10, pp. 1992–1998, May 2012, doi: 10.2514/3.12243.

[6] W. C. Park, “Numerical investigation of wake flow control by a splitter plate,” KSME Int. J., vol. 12, no. 1, pp. 123–131, 1998, doi: 10.1007/BF02946540/METRICS.

[7] C. Dalton, Y. Xu, and J. C. Owen, “THE SUPPRESSION OF LIFT ON A CIRCULAR CYLINDER DUE TO VORTEX SHEDDING AT MODERATE REYNOLDS NUMBERS,” J. Fluids Struct., vol. 15, no. 3–4, pp. 617–628, Apr. 2001, doi: 10.1006/JFLS.2000.0361.

[8] R. M. Darekar and S. J. Sherwin, “FLOW PAST A BLUFF BODY WITH A WAVY STAGNATION FACE,” J. Fluids Struct., vol. 15, no. 3–4, pp. 587–596, Apr. 2001, doi: 10.1006/JFLS.2000.0354.

[9] T. Tsutsui, T. & Igrashi, “Drag Reduction of a Circular rod in an Air-Stream,” J. Wind Eng. Ind. Aerodyn., vol. 4, no. 5, pp. 527–54, 2002.

[10] G. R. Vamsee, M. L. De Tena, and S. Tiwari, “Effect of arrangement of inline splitter plate on flow past square cylinder,” Prog. Comput. Fluid Dyn., vol. 14, no. 5, pp. 277–294, 2014, doi: 10.1504/PCFD.2014.064554.

[11] S. U. Islam, H. Rahman, W. S. Abbasi, and T. Shahina, “Lattice Boltzmann Study of Wake Structure and Force Statistics for Various Gap Spacings Between a Square Cylinder with a Detached Flat Plate,” Arab. J. Sci. Eng., vol. 40, no. 8, pp. 2169–2182, Aug. 2015, doi: 10.1007/S13369-015-1648-3/METRICS.

[12] R. Simenthy, V. Raghavan, and S. Tiwari, “Effect of Downstream Flapping Plate on the Flow Field Characteristics behind a Circular Cylinder,” no. 169.

[13] C. Y. Zhou, L. Wang, and W. Huang, “Numerical study of fluid force reduction on a circular cylinder using tripping rods,” J. Mech. Sci. Technol., vol. 21, no. 9, pp. 1425–1434, 2007, doi: 10.1007/BF03177429/METRICS.

[14] Q. D. Shao, C.P. & Wei, “Control of vortex shedding from a main rod,” AIAA J., vol. 46, pp. 397–407, 2008.

[15] C. H. Kuo and C. C. Chen, “Passive control of wake flow by two small control cylinders at Reynolds number 80,” J. Fluids Struct., vol. 25, no. 6, pp. 1021–1028, Aug. 2009, doi: 10.1016/J.JFLUIDSTRUCTS.2009.05.007.

[16] H. Wu, D. P. Sun, L. Lu, B. Teng, G. Q. Tang, and J. N. Song, “Experimental investigation on the suppression of vortex-induced vibration of long flexible riser by multiple control rods,” J. Fluids Struct., vol. 30, pp. 115–132, Apr. 2012, doi: 10.1016/J.JFLUIDSTRUCTS.2012.02.004.

[17] M. S. M. Ali, C. J. Doolan, and V. Wheatley, “Low Reynolds number flow over a square cylinder with a detached flat plate,” Int. J. Heat Fluid Flow, vol. 36, pp. 133–141, Aug. 2012, doi: 10.1016/J.IJHEATFLUIDFLOW.2012.03.011.

[18] A. Gupta and A. K. Saha, “Suppression of vortex shedding in flow around a square cylinder using control cylinder,” Eur. J. Mech. - B/Fluids, vol. 76, pp. 276–291, Jul. 2019, doi: 10.1016/J.EUROMECHFLU.2019.03.006.

[19] R. S. Serson, D., Meneghini, J.R., Carmo, B.S., Volpe, E. V. & Gioria, “Wake transition in the flow around a circular rod with a splitter plate,” J. Fluid Mech, vol. 755, pp. 582–602, 2014.

[20] L. Lu et al., “Numerical investigation of fluid flow past circular cylinder with multiple control rods at low Reynolds number,” J. Fluids Struct., vol. 48, pp. 235–259, Jul. 2014, doi: 10.1016/J.JFLUIDSTRUCTS.2014.03.006.

[21] S. U. Islam, H. Rahman, W. S. Abbasi, U. Noreen, and A. Khan, “Suppression of fluid force on flow past a square cylinder with a detached flat plate at low Reynolds number for various spacing ratios,” J. Mech. Sci. Technol., vol. 28, no. 12, pp. 4969–4978, Dec. 2014, doi: 10.1007/S12206-014-1118-Y/METRICS.

[22] S. U. Islam, R. Manzoor, Z. U. Islam, S. Kalsoom, and Z. C. Ying, “A computational study of drag reduction and vortex shedding suppression of flow past a square cylinder in presence of small control cylinders,” AIP Adv., vol. 7, no. 4, Apr. 2017, doi: 10.1063/1.4982696/22101.

[23] S. U. Islam, R. Manzoor, and C. Y. Zhou, “Effect of Reynolds Numbers on Flow Past a Square Cylinder in Presence of Multiple Control Cylinders at Various Gap Spacings,” Arab. J. Sci. Eng., vol. 42, no. 3, pp. 1049–1064, Mar. 2017, doi: 10.1007/S13369-016-2302-4/METRICS.

[24] D. T. Sukop, M. C. & Thorne, “Lattice Boltzmann modeling: an introduction for scientists and Engineers,” Springer Berlin Heidelb., 2005.

[25] D. A. Wolf-Gladrow, “Lattice-gas cellular automata,” pp. 39–138, 2000, doi: 10.1007/978-3-540-46586-7_3.

[26] T. G. Chapman, S., Cowling, “Mathematical Theory of Non-Uniform Gases,” Cambridge Univ. Press. Third Ed., 1970.