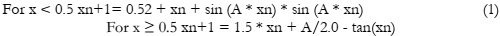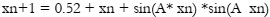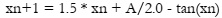Revolutionizing Cryptography: A Cutting-Edge Substitution Box Design Through 
Trigonometric Transformation

Awais Ahmed Qarni; Kashif Ishaq; Naeem A. Nawaz; Ghulam Mustafa; Muhammad Fahad

Revolutionizing Cryptography: A Cutting-Edge Substitution Box Design Through Trigonometric Transformation

Qarni. A. A¹, Ishaq. K¹, Nawaz. N. A¹, Mustafa. G¹, Fahad. M²

¹ School of Systems and Technology, University of the Management and Technology, Lahore, Pakistan

² Department of Computer Engineering, University of Engineering and Technology, Lahore, Pakistan

Abstract
This paper proposes an innovative approach to enhance the robustness of substitution boxes in cryptography by employing chaotic mapping. Our methodology leverages chaotic mapping to construct a robust 8 × 8 S-box that adheres to the requirements of a bijective function. An illustrative example of such an S-box is presented, accompanied by a comprehensive analysis employing established metrics such as nonlinearity, bijection, bit independence, strict avalanche effect, linear approximation probability, and differential uniformity. To evaluate its strength, we benchmark the performance of our proposed S-box against recently investigated counterparts. Our findings reveal that our approach to S-box construction is both pioneering and efficacious in fortifying substitution boxes for cryptography. Given the escalating frequency of cyber threats and hacking incidents, safeguarding online communication and personal information has become increasingly challenging. Cryptography plays a pivotal role in addressing these challenges by transforming data into a more secure format. In this research, we introduce a novel, lightweight algorithm grounded in trigonometric principles, which significantly enhances security and reduces susceptibility to hacking attempts. Comparative evaluations demonstrate the superior performance of our algorithm over established methods such as the Hill cipher, Blowfish, and DES. While conventional approaches prioritize security, they often incur delays due to increased computational load. Our objective is to expedite cryptographic processes without compromising security, achieved through the strategic application of trigonometric principles. Our algorithm capitalizes on trigonometric functions and operations to introduce confusion, thereby thwarting hacking attempts. Extensive research and testing substantiate that our algorithm excels in both security and speed compared to traditional methods. By seamlessly integrating trigonometric concepts into a streamlined design, our algorithm proves to be practical for real-world applications, offering a robust solution for safeguarding data on the Internet.

Keywords: Substitution-Box, Linear Trigonometric Transformation, Security, Cryptosystems.

Corresponding Author	How to Cite this Article
Awais Ahmed Qarni, School of Systems and Technology, University of the Management and Technology, Lahore, Pakistan	Awais Ahmed Qarni, Kashif Ishaq, Naeem A. Nawaz, Ghulam Mustafa, Muhammad Fahad , Revolutionizing Cryptography: A Cutting-Edge Substitution Box Design Through Trigonometric Transformation. IJIST. 2023 ;5(4):730-745 https://journal.50sea.com/index.php/IJIST/article/view/592

Introduction

In today's world, most information exists in digital form, and even the remaining hard copies are transitioning to digital. This shift has brought numerous advantages, allowing people to communicate online and share data using various platforms. The data sources are not just what individuals intentionally share online; they also include personal information, data generated by algorithms on platforms, and data from communications, whether between platforms or individuals, groups, organizations, or even governments [1]. However, digital data poses significant privacy risks if not properly managed and secured. Malicious individuals are always seeking such data to exploit and harm individuals, organizations, or even entire nations. Therefore, technology experts continually work on making these technologies secure and reliable because data security is a major concern. The use of encoding and decoding techniques has historical significance, often used in times of war to transmit intelligence messages on the battlefield. There's a growing need to revive these techniques to instill confidence in end-users, especially in cloud environments [2]. The key objective is to ensure that data remains inaccessible to unauthorized individuals. If someone manages to access the data, it should be in a form that is difficult for them to understand, requiring a significant amount of time and effort. Organizations and technology experts are dedicated to establishing rules and procedures that not only protect the confidentiality of data but also ensure its integrity [3]. Once these procedures are in place, malicious actors find it challenging to decode or access the data.

Cryptography:

Cryptography is a way to protect information by turning it into a secret code. It's an important tool for keeping data safe. Many projects with large budgets are dedicated to making cryptography techniques harder to break by attackers. Cryptography involves two main steps: encryption and decryption. In encryption, plain text is transformed into an unreadable form, and it can be turned back into plain text through decryption using specific rules. Initially, only mathematics and computer science were used in developing encryption methods, but over time, electrical engineering and even physics and its subfields have been incorporated to make it more challenging for malicious actors to compromise. Cryptanalysis is a research field that focuses on studying encryption techniques to find weaknesses that could be exploited by attackers [4]. Those who want to break into systems are often the ones conducting this research. Today, government agencies and law enforcement use encryption to investigate crimes within their own country and to monitor the activities of other nations [5]. Additionally, cloud service providers and e-commerce websites use advanced encryption to protect the privacy and data integrity of their users. They compete to provide the most secure infrastructure and maintain the trust of their customers.

Fundamental of Cryptography:

Cryptography is based on four important principles:

Confidentiality:

This means that only authorized people can access certain data. Others who are not authorized won't be able to understand the data, even if they somehow gain access. For instance, only I can access my online banking account.

Data Integrity:

Data integrity ensures that the data is accurate and consistent. It's not just about the data itself but also about the systems that store the data. Sometimes, the data can be corrected, but if the system is not reliable, it can lead to inconsistencies.

Authentication:

Authentication is about confirming that the person trying to access the data is who they claim to be. For example, before I can log into my online banking account, the system checks that I'm the authorized user by verifying my credentials.

Non-Repudiation:

The fourth one is non-repudiation; this term means that the person who modified or accessed the data cannot deny his action. For example, I have made some changes i.e., withdraw cash or made some online purchases and at the time of reconciliation I refused to make those payments then my logs will be provided as proof.

Types of Cryptography:

Cryptography comes in three main types:

Symmetric Cryptography:

In this method, the same key is used to both encrypt and decrypt information. The security relies on the length of the key [6]. The challenge here is how to securely share the key with the recipient. If it's sent through the same communication channel, that channel's security also becomes crucial.

Asymmetric Cryptography:

This type uses two keys – a public key and a private key. The sender uses their private key and the recipient's public key to encrypt the data. The recipient uses their private key and the sender's public key to decrypt it. Asymmetric cryptography helps solve the key distribution problem present in symmetric cryptography.

Hashing:

Hashing involves converting sensitive information into a fixed-length hash using a hash function. The efficiency of this process depends on the quality of the hash function. Hashing ensures that data remains intact during transmission, without any chance of alteration [7].

As organizations establish procedures to secure data, a new challenge arises — ensuring the security of these procedures themselves against potential breaches by malicious actors. Cryptography plays a pivotal role in this endeavor, transforming messages or classified data from a basic language into an unintelligible form. It has become a crucial element in ensuring information security, with substantial funding dedicated to making cryptographic methods increasingly resilient to attacks. The advent of cryptographic algorithms such as DES and AES introduced the significance of the S-box, a key-dependent formulation crucial in their procedures. The S-box, responsible for mutating input data into a newly shaped output, proves resistant to both linear and differential cryptanalysis techniques. Emphasizing attributes of confusion and diffusion, the strength of an S-box correlates with its robustness. S-boxes are categorized into two modes: Static S-boxes, publicly defined within the algorithm's procedure, are easily accessible but vulnerable to reverse engineering. In contrast, Dynamic S-boxes address this vulnerability by being generated with the aid of a secret key, ensuring secure communication over public channels. This evolution is particularly significant in the field of cybersecurity, with researchers investing significant resources in its advancement. To evaluate S-box security, various tests are conducted, including algebraic degree and differential uniformity. The algebraic degree measures the complexity of the S-box function through its polynomial value, while differential uniformity assesses the XOR operation on various pairs of S-boxes. These tests contribute to verifying the effectiveness and security of the S-box design [8].

The paper is organized as follows: In Section 2, we examine established techniques related to substitution boxes. Section 3 provides detailed insights into our proposed substitution method. Section 4 presents the experimental results and comparisons with contemporary techniques. Lastly, Section 5 covers the conclusion and potential avenues for future research.

Literature Review:

S-box cryptography is a significant concept in current symmetric key cryptography, representing the heart of substitution-permutation networks (SPNs) used in popular block ciphers like the Advanced Encryption Standard (AES) [9]. The subsite- tuition box (S-box) is important to S-box cryptography. It is a mathematical entity or table that performs nonlinear replacements, infusing complexity into data changes. This complexity encourages the obfuscation of the connection between input and output, increasing the complexity of cryptographic processes and enhancing security. Nonlinearity to prevent algebraic deductions, the avalanche effect to accent-tube output discrepancies caused by minor input changes, and resistance to differential and linear cryptanalysis are all important characteristics of robust S-boxes. These features combine to constitute a cornerstone in the design of robust encryption algorithms, as demonstrated by the use of S- S-boxes inside them [10]. Mathematicians refer to the complex and erratic behaviors that nonlinear dynamical systems display as chaos. These behaviors are distinguished by their sensitivity to the beginning conditions, leading to erroneous oscillations, bifurcations, and the appearance of odd attractors. Chaotic systems are useful in many fields, including physics, biology, chemistry, engineering, and economics because they are good models for a variety of phenomena. Notably, secure common-nidation, data encryption, and signal processing are among the practical applications of chaotic systems. Due to their fundamental structure and their importance in cryptography, one-dimensional (1D) [10] chaotic systems have attracted a lot of attention. However, it has been shown that the majority of 1D chaotic systems have a limited spectrum of chaos. Given this restriction, investigating compound chaotic maps becomes an appealing option. Particularly in the field of cryptography, these compound maps have the singular capacity to provide enhanced chaotic behaviors and increased security in a variety of applications [11]. Due to their fundamental structure and their importance in cryptography, one-dimensional (1D) chaotic systems have attracted a lot of attention. However, it has been shown that the majority of 1D chaotic systems have a limited spectrum of chaos. Given this restriction, investigating com- pound chaotic maps becomes an appealing option. Particularly in the field of cryptography, these compound maps have the singular capacity to provide enhanced chaotic behaviors and increased security in a variety of applications.

A substantial amount of research is being carried out in the cryptography domain; one of the hot topics is the substitution box (S-box). Bukhari et al [5]. proposed a novel model to encrypt grayscale images using an S-box. The proposed approach uses the Galois field and linear fractional transformations to generate six different S-boxes and then use them for gray-scale image encryption. Shah and Shah [12] developed a new method for creating sixteen (16) distinct robust 8 × 8 S-boxes using sixteen extensions of the Galois field GF (28). In the proposed methodology, sixteen linear fractional transformations were defined against those Galois fields. To improve the encryption strength of AES [12]. Employed the chaotic logistic map, Mobius transformation, and symmetric group S256 to create a dynamic S-box [13] proposed a 24× 24 S-box. For generating the proposed S-box, the maximal cyclic subgroup of the multiplicative group of Galois ring unit GR (23, 8) was used. The Proposes-box has better confusion potential than that of any 8 × 8 S-boxes. The authors used the proposed S-box in encryption to induce confusion in RGB channels of a plain image. 24 × 24 S-box dependent encryption method outperformed the 8 × 8 S-box dependent encryption method [12] and presented a technique for generating an S-box utilizing a module of a group of PSL (2, Z) on projective line PL(F257) over Galois Field GF (28). The obtained results were compared with relevant S-Boxes. Researchers [14] presented a new way to design and construct cryptographically strong 8 × 8 S-boxes for block ciphers utilizing a linear fractional transformation and a permutation function over the GF (28).

Material and Method

Proposed Methodology:

Those block ciphers designed via chaotic maps show more. On-linearity and efficiency when compared with commonly known ciphers. LMs based on CM as one of the fields of mathematics require complex mathematical calculations to design a formula for encryption [3]. The formula prepared for this thesis work is based on CM, a key-dependent mechanism developed to prepare a dynamic S-box. The chaos property of CM is widely used to develop entropy, this feature generates the properties of confusion and diffusion [5]. When the chaotic parameters along with the encryption key are merged system- antically, it becomes almost impossible for attackers to predict the key or plain text from the output [12]. S-box Construction Process In this Paperwork, a unique formula was devised to produce a dynamic S-box. The process of new dynamic S-Box generation comprises the following steps: New Chaotic Map Design and Elementary S-Box Development

New Chaotic Map Design:

The new chaotic map designed is mathematically stated in Equation (1).

This study presents a methodology for constructing S-boxes using iterative equations based on chaotic maps. The construction involves two cases: one for x < 0.5 and another for x > 0.5. Let's break down each case:

Case 1: x < 0.5

The iterative equation for this case is given by:

Explanation:

• xn represents the current value in the sequence.

• The term 0.52 + xn introduces a constant and the current value to the next iteration.

• The sinusoidal component sin(A* xn) sin(A*xn) adds a non-linear and chaotic element to the iteration.

Case 2: (x > 0.5)

The iterative equation for this case is given by:

Explanation:

• xn again represents the current value in the sequence.

• 1.5 *xn introduces a linear component, scaling the current value.

• A/2.0 adds a constant term.

• tan(xn) contributes a non-linear element.

These equations employ chaotic map principles to generate sequences of values for constructing S-boxes. The non-linear components introduced through sine and tangent functions enhance the cryptographic properties of the resulting S-box. It's essential to note that \(A\) is a parameter whose value influences the behavior of the chaotic map and, consequently, the generated S-box.

Bifurcation:

Bifurcation is the analysis of the subjective and topographical transformation of the phase space of a system that results from parameter adjustments and has a significant threshold. Solid lines represent steady values while dotted lines represent unstable values [13]. The majority of the time, a slight modification in parameters causes a significant fluctuation in system performance with a topologically altered phase space. The bifurcation diagram plots the change of the control parameter on the horizontal axis against the sampled steady-state values of one of the variables on the vertical axis. A logistic map (LM) is a one-dimensional chaotic map that displays bifurcation and chaos. It is defined in Equation (2).

The control parameter α determines how chaotically the logistic map behaves, and its limit is between [0, 4]. Likewise, Tent Map (TM) is also a one-dimensional chaotic map that exhibits bifurcation and chaotic behavior. It is defined in Equation (3).

The control parameter μ controls the chaotic behavior of the tent map, and its limit is between [0, 4]. The bifurcation results of these 3 chaotic maps (LM, TM, and proposed chaotic map) are compared and shown in Figure 1. The comparison shows that the bifurcation behavior of the proposed chaotic map is better and covers more area as compared to LM and TM [13].

Figure 1: Bifurcation test results of (a) Logistic map, (b) Tent map, and (c) Proposed chaotic map

Lyapunov Exponent:

For the purpose of describing chaos, an analytical metric known as the Lyapunov-Exponent (LE) is utilized. The system is chaotic if the chaotic map of the system has a Lyapunov exponent that is greater than 0. The instability of the system increases in proportion to the value of LE. The rate at which the unseen approximation is either converging or diverging is disclosed by the LE. In cryptography, the idea of Lyapunov exponents can also be utilized for the purpose of performing analysis on substitution boxes, commonly known as S-boxes. S-boxes, which are essential elements of symmetric key block ciphers, are the ones accountable for the non-linearity and confusion that are introduced throughout the encryption process. By gaining an understanding of the Lyapunov exponents of S-boxes, one can gain insights into the dynamical behavior and security properties of these structures. In order to use the Lyapunov exponents with S-boxes, we must first think of the S-box as a discrete dynamical system. The input to the S-box is a binary vector, and the output is also a binary vector that is created by applying the S-box transformation. Both vectors can be expressed using the same notation. After that, we will be able to investigate how slight alterations in the input are transmitted across the S-box and impact the output [14].

Figure 2: Lyapunov exponent results of (a) LM, TM, and (c) Proposed chaotic map [15]

Elementary S-Box Development:

First, an initial value of 15 decimal places is selected as Xn. The range of Xn is 0 to 1. This value goes through one of the two conditions, depending on the value that is selected to obtain the next value Xn+1. After that, the value is rounded to obtain an absolute value. These positive values are then stored in Y and MOD 256 is applied to these values. A variable LOC with a range of 0 to 255 is taken that will specify the location where the values will be added to the array. The initial value of LOC is 0. An array S’ of length 256 is taken which is initially filled with 0. The value stored in Y is added to array S’ if it previously did not exist in the array. Then this value is added to array S which is the elementary S-Box, and LOC is incremented by 1 [16]. If the value Y already exists in the S’ array, then it is skipped, and the process is repeated till all 256 values are obtained.

Algorithm 1: Initial S-Box

To better understand the process of the chaotic map, Figure 3 shows the flowchart for the generation of elementary S-Box

Figure 3: Flowchart for Elementary S-Box Design [15]

Elementary S-Box is given below in Table 1 using value.

Xn = 0.332031250 < A < 1

Table 1: Elementary S-Box

Initial values for the secondary S-Box generation are given below.

A = 374237

B = 159731

Xn = 0.069656344173072

R = 2.871745947223140

Table 2: Secondary S-Box

Result and Discussion

A significant data and information research contribution. The development of new S-boxes is central to the security field. After an S-box is created, it is examined to determine its. The ability to choose how strong it will be against various attacks. (Differential and linear) [17]. There are tests for an S-Box’s cryptanalytic evaluation. Calculated using the predetermined criteria, which include:

a. Nonlinearity (NL)

b. Fixed Points

c. Bit Independence Criterion

d. Strict Avalanche Criterion.

e. Linear Approximation Probability

f. Differential Approximation Probability

Nonlinearity:

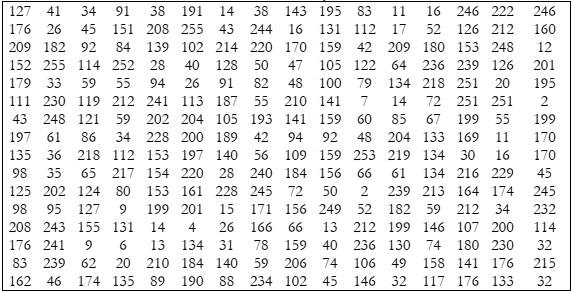
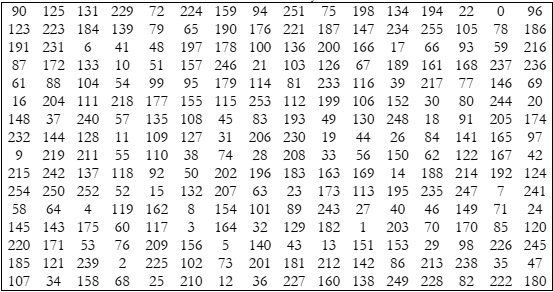
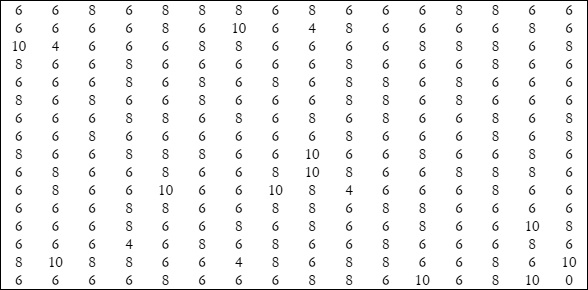
In general, the capacity to withstand a linear cryptanalysis attack increases with the value of nonlinearity. The nonlinearity values of the proposed S-Box are 110, 110, 112, 108, 108, 110, 110, and 110, with the smallest value of 108, the largest value of 112, and an average value of 109.75. The nonlinearity values of the proposed S-Box are mentioned in Table 3.

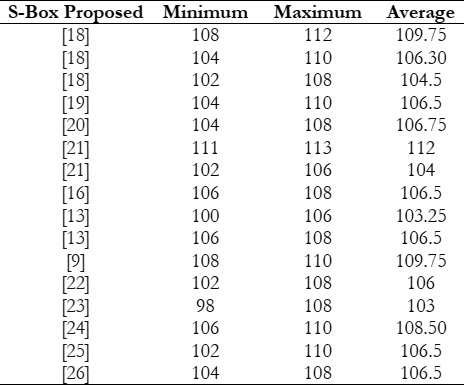
Table 3: Nonlinearity values of Proposed S-BOX

A comparison with nonlinearity values of some recent S-Boxes is shown in Table 4. It is clear that the proposed S-Box has a higher average value of NL than most of the S-Boxes.

Table 4: Comparison of Nonlinearity (NL) With Recent S-Boxes

Fixed Points:

When an input value and its corresponding output value are the same, an S-box fixed point. Fixed Points may induce flaws and lessen the algorithm's security. One of the causes is that a fixed point may enable an attacker to deduce details about the input or output values based on the relationship between the fixed point and the known input or output values. To ensure security, the proposed S-Box was tested against a fixed point criterion. Table 2 shows that there is no fixed point in the proposed S-Box. There is no opposite fixed point in the proposed S-Box as well [27].

Bit Independence Criterion (BIC):

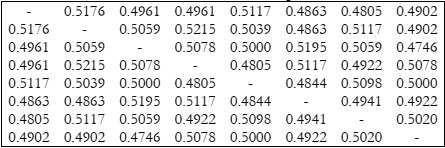
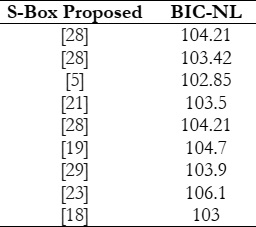
Normally, the statistical correlation between the corresponding output bit patterns and all potential input bit patterns is taken into account while evaluating the BIC [19]. A statistically balanced distribution of output bit patterns is desired in order to guarantee the absence of bias and predictable relationships. Table 5 shows the BIC-NL values of the proposed S-Box. The average value of BIC-NL is 104.21.

Table 5: BIC-NL values of proposed S-Boxes

Table 6: BIC-SAC Matrix of Proposed S-Box

A comparison with average BIC-NL values of some recent S-Boxes is shown in Table 7.

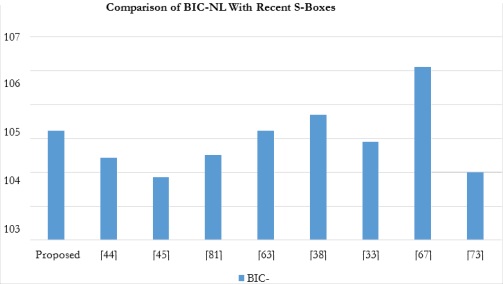
Table 7: Comparison of BIC-NL With Recent S-Boxes

The BIC-NL visualization results of the proposed S-Box with other previously designed S-Boxes are shown in Figure 4. After comparison, it is clear that the average BIC-NL value of the proposed S-Box 104.21 is higher than most of the other S-Boxes it is compared with.

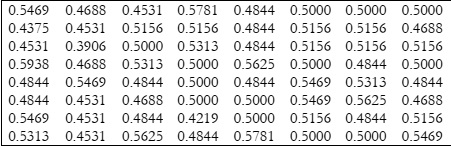
Figure 4: Comparison of BIC-NL with recent S-Boxes

Strict Avalanche Criterion:

The strict avalanche criteria (SAC) describes how output behaves, and SAC is satisfied only when anyone complements a single input bit, changing half of the output bits [20]. A single change to the input value should toggle half of the output bit in order to satisfy SAC. As the substitution permutation recurrence advances, a single modification in the input bit will result in an avalanche change. Each of the output bits in the S-Box should alter with a probability of 0.5 if a single input bit changes. The average SAC value of the proposed S-Box is 0.5017.

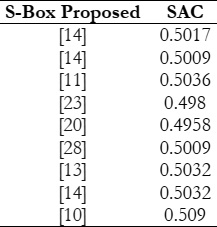
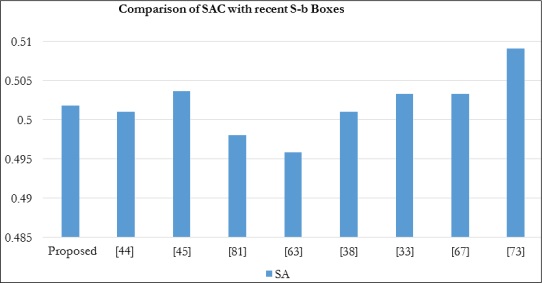
Table 8: SAC Dependency Matrix of Proposed S-Box

A comparison with average SAC values of some recent S-Boxes is shown in Table 9.

Table 9: Comparison of SAC With Recent S-Boxes

The SAC visualization results of the proposed S-Box with other previously designed S-Boxes are shown in Figure 5. After comparison, it is clear that the average SAC value of the proposed S-Box which is 0.5017 is more accurate than most of the other S-Boxes it is compared with [29].

Figure 5: Comparison of SAC with recent S-Boxes

Linear Approximation Probability:

Table 10: Comparison of LP With Recent S-Boxes

When the input and output of an S-box are linearly connected, the correlation between the input and output bits is measured by the linear approximation probability [21]. A numeric value between 0 and 0.5 is commonly used to denote the linear approximation probability. Significant linear approximation, or a score approaching 0.5, denotes a significant correlation between the linear relationship and the S-box behavior. 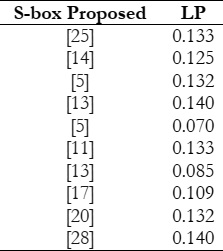The correlation is low if the value is close to 0, which denotes a poor linear approximation [24]. The average LP of the proposed S-Box is 0.1329. A comparison with average LP values of some recent S-Boxes is shown in Table 10.

Differential Approximation Probability:

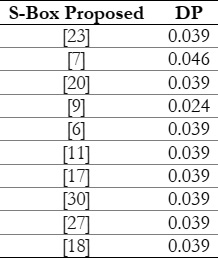
A numeric value between 0 and 1 is commonly used to denote the differential approximation probability. The input and output differences have a strong association when their values are close to 1, which could point to a weakness in the linear approximation [28]. A correlation that is weak and close to 0 suggests nonlinear behavior and greater susceptibility to differential cryptanalysis. The average DU value is 0.0391. Table 11 shows the differential uniformity of the proposed S-Box [22].

Table 11: DU Matrix of Proposed S-Box

A comparison with average DP values of some recent S-Boxes is shown in Table 12.

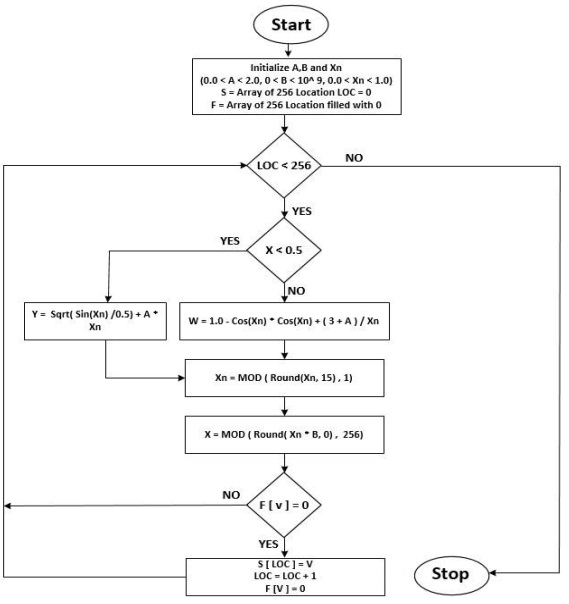
Table 12: Comparison of DP Values with Recent S-Boxes

Efficiency Analysis:

On a machine running Windows 7 with 6GB of Memory and a 2.24GHz Intel Core i5 Processor, to assess the computational efficiency of the suggested S-box approach, a Visual C simulation was done [30]. The suggested method’s calculation efficiency was observed for both the initial and final S-boxes. A clever and heuristic approach for calculating the initial S- S-cryptographic box’s strength is necessary for the S-creation. box’s 100000 distinct beginning S-boxes were produced in order to assess their time complexity and the time needed to the average time complexity of these initial and final S-box constructions is measured in Table 10. Table 10 demonstrates how highly motivating the preliminary S-building box’s time is. However, the proposed solution requires a little more time to build an S-box.

Conclusion

There are two popular design approaches for creating S- S-boxes: chaos-based and Trigonometric Transformation theory-based. The security benefits of each of these design paradigms are distinct. application. In this article, we compare the two approaches and propose a way to construct a non-bijective S-box. The proposed improved chaos map of this method is used for the chaotic heuristic search of the first S-box. The security properties of the generated bijective S-boxes are improved by a proposed strong group created after extensive experiments [23]. Algebraic group actions improvise cryptographic properties of S-boxes. Based on experimental results. findings, the suggested S-boxes adequately met the requirements for competent S-boxes. The ability to build highly nonlinear, Variable-sized S-boxes is an advantage of the proposed S-box generation method. Another advantage of this method is that it yields the highest nonlinearity score of 109.5 for an S-box of any of the available S-boxes [18]. Additionally, S-boxes of recent proposals are used in the comparative analysis to determine the overall standing. Comparing the proposed bijective S-boxes to the majority of the existing S-boxes, it has been discovered that they have superior nonlinearity, SAC, and linear approximation probability features. In future work, it would be valuable to explore the practical implications and applications of the proposed non-bijective S-box construction method. Further investigations could focus on assessing the real-world performance of the suggested improved chaos map and its impact on cryptographic applications. Additionally, the role of the proposed strong group in enhancing the security properties of the generated bijective S-boxes could be further explored and validated through extensive practical experiments.

Machine learning plays a pivotal role in advancing diverse fields [31][32][33][34][35][36][37][38][39][40][41][42][43][44][45], including cryptography. Building on this foundation, we plan to harness machine learning for an innovative design of a substitution box, employing trigonometric transformations to enhance security and resilience in encryption methods as future work.

Reference

[1] S. Xu, Y. Wang, Y. Guo, and C. Wang, “A novel chaos-based image encryption scheme,” Proc. - 2009 Int. Conf. Inf. Eng. Comput. Sci. ICIECS 2009, 2009, doi: 10.1109/ICIECS.2009.5365275.

[2] S. Bukhari, A. Yousaf, S. Niazi, and M. R. Anjum, “A Novel Technique for the Generation and Application of Substitution Boxes (s-box) for the Image Encryption,” Nucl., vol. 55, no. 4, pp. 219–225, 2018, Accessed: Dec. 09, 2023. [Online]. Available: http://thenucleuspak.org.pk/index.php/Nucleus/article/view/229

[3] M. Ge and R. Ye, “A novel image encryption scheme based on 3D bit matrix and chaotic map with Markov properties,” Egypt. Informatics J., vol. 20, no. 1, pp. 45–54, Mar. 2019, doi: 10.1016/J.EIJ.2018.10.001.

[4] I. Hussain, A. Anees, T. A. Al-Maadeed, and M. T. Mustafa, “Construction of S-Box Based on Chaotic Map and Algebraic Structures,” Symmetry 2019, Vol. 11, Page 351, vol. 11, no. 3, p. 351, Mar. 2019, doi: 10.3390/SYM11030351.

[5] W. Yan and Q. Ding, “A Novel S-Box Dynamic Design Based on Nonlinear-Transform of 1D Chaotic Maps,” Electron. 2021, Vol. 10, Page 1313, vol. 10, no. 11, p. 1313, May 2021, doi: 10.3390/ELECTRONICS10111313.

[6] S. Shaukat Jamal, D. Shah, A. Deajim, and T. Shah, “The Effect of the Primitive Irreducible Polynomial on the Quality of Cryptographic Properties of Block Ciphers,” Secur. Commun. Networks, vol. 2020, 2020, doi: 10.1155/2020/8883884.

[7] X. Zhang et al., “Generation and Evaluation of a New Time-Dependent Dynamic S-Box Algorithm for AES Block Cipher Cryptosystems,” IOP Conf. Ser. Mater. Sci. Eng., vol. 978, no. 1, p. 012042, Nov. 2020, doi: 10.1088/1757-899X/978/1/012042.

[8] V. Kumar and A. Girdhar, “A 2D logistic map and Lorenz-Rossler chaotic system based RGB image encryption approach,” Multimed. Tools Appl., vol. 80, no. 3, pp. 3749–3773, Jan. 2021, doi: 10.1007/S11042-020-09854-X/METRICS.

[9] X. yuan Wang and Q. Yu, “A block encryption algorithm based on dynamic sequences of multiple chaotic systems,” Commun. Nonlinear Sci. Numer. Simul., vol. 14, no. 2, pp. 574–581, Feb. 2009, doi: 10.1016/J.CNSNS.2007.10.011.

[10] S. Hanis and R. Amutha, “A fast double-keyed authenticated image encryption scheme using an improved chaotic map and a butterfly-like structure,” Nonlinear Dyn., vol. 95, no. 1, pp. 421–432, Jan. 2019, doi: 10.1007/S11071-018-4573-7/METRICS.

[11] H. Gao, Y. Zhang, S. Liang, and D. Li, “A new chaotic algorithm for image encryption,” Chaos, Solitons & Fractals, vol. 29, no. 2, pp. 393–399, Jul. 2006, doi: 10.1016/J.CHAOS.2005.08.110.

[12] X. Wang and D. Chen, “A parallel encryption algorithm based on piecewise linear chaotic map,” Math. Probl. Eng., vol. 2013, 2013, doi: 10.1155/2013/537934.

[13] N. A. Khan, M. Altaf, and F. A. Khan, “Selective encryption of JPEG images with chaotic based novel S-box,” Multimed. Tools Appl., vol. 80, no. 6, pp. 9639–9656, Mar. 2021, doi: 10.1007/S11042-020-10110-5/METRICS.

[14] L. C. Nizam Chew and E. S. Ismail, “S-box Construction Based on Linear Fractional Transformation and Permutation Function,” Symmetry 2020, Vol. 12, Page 826, vol. 12, no. 5, p. 826, May 2020, doi: 10.3390/SYM12050826.

[15] K. Ishaq and A. A. Qarni, “An Innovative Design of Substitution Box Using Trigonometric Transformation,” Aug. 2023, Accessed: Dec. 26, 2023. [Online]. Available: https://arxiv.org/abs/2311.16107v1

[16] H. Liu, B. Zhao, and L. Huang, “Quantum Image Encryption Scheme Using Arnold Transform and S-box Scrambling,” Entropy 2019, Vol. 21, Page 343, vol. 21, no. 4, p. 343, Mar. 2019, doi: 10.3390/E21040343.

[17] K. Z. Zamli, “Optimizing S-box generation based on the Adaptive Agent Heroes and Cowards Algorithm,” Expert Syst. Appl., vol. 182, p. 115305, Nov. 2021, doi: 10.1016/J.ESWA.2021.115305.

[18] X. Wang et al., “S-Box Based Image Encryption Application Using a Chaotic System without Equilibrium,” Appl. Sci. 2019, Vol. 9, Page 781, vol. 9, no. 4, p. 781, Feb. 2019, doi: 10.3390/APP9040781.

[19] X. Wang, J. Yang, and N. Guan, “High-sensitivity image encryption algorithm with random cross diffusion based on dynamically random coupled map lattice model,” Chaos, Solitons & Fractals, vol. 143, p. 110582, Feb. 2021, doi: 10.1016/J.CHAOS.2020.110582.

[20] M. Ahmad, E. Al-Solami, A. M. Alghamdi, and M. A. Yousaf, “Bijective S-Boxes Method Using Improved Chaotic Map-Based Heuristic Search and Algebraic Group Structures,” IEEE Access, vol. 8, pp. 110397–110411, 2020, doi: 10.1109/ACCESS.2020.3001868.

[21] H. Alsaif, R. Guesmi, A. Kalghoum, B. M. Alshammari, and T. Guesmi, “A Novel Strong S-Box Design Using Quantum Crossover and Chaotic Boolean Functions for Symmetric Cryptosystems,” Symmetry 2023, Vol. 15, Page 833, vol. 15, no. 4, p. 833, Mar. 2023, doi: 10.3390/SYM15040833.

[22] Z. Jiang and Q. Ding, “Construction of an S-Box Based on Chaotic and Bent Functions,” Symmetry 2021, Vol. 13, Page 671, vol. 13, no. 4, p. 671, Apr. 2021, doi: 10.3390/SYM13040671.

[23] M. F. Khan, K. Saleem, M. A. Alshara, and S. Bashir, “Multilevel information fusion for cryptographic substitution box construction based on inevitable random noise in medical imaging,” Sci. Reports 2021 111, vol. 11, no. 1, pp. 1–23, Jul. 2021, doi: 10.1038/s41598-021-93344-z.

[24] Q. Lu, C. Zhu, and X. Deng, “An Efficient Image Encryption Scheme Based on the LSS Chaotic Map and Single S-Box,” IEEE Access, vol. 8, pp. 25664–25678, 2020, doi: 10.1109/ACCESS.2020.2970806.

[25] X. Liu, X. Tong, Z. Wang, and M. Zhang, “Efficient high nonlinearity S-box generating algorithm based on third-order nonlinear digital filter,” Chaos, Solitons & Fractals, vol. 150, p. 111109, Sep. 2021, doi: 10.1016/J.CHAOS.2021.111109.

[26] M. Ahmad, U. Shamsi, and I. R. Khan, “An Enhanced Image Encryption Algorithm Using Fractional Chaotic Systems,” Procedia Comput. Sci., vol. 57, pp. 852–859, Jan. 2015, doi: 10.1016/J.PROCS.2015.07.494.

[27] “Image Encryption based on Chaotic Map and Reversible Integer Wavelet Transform.” Accessed: Dec. 09, 2023. [Online]. Available: https://sciendo.com/article/10.2478/jee-2014-0013

[28] A. Razzaque et al., “An efficient S-box design scheme for image encryption based on the combination of a coset graph and a matrix transformer,” Electron. Res. Arch. 2023 52708, vol. 31, no. 5, pp. 2708–2732, 2023, doi: 10.3934/ERA.2023137.

[29] L. Liu, Y. Zhang, and X. Wang, “A Novel Method for Constructing the S-Box Based on Spatiotemporal Chaotic Dynamics,” Appl. Sci. 2018, Vol. 8, Page 2650, vol. 8, no. 12, p. 2650, Dec. 2018, doi: 10.3390/APP8122650.

[30] F. ul Islam and G. Liu, “Designing S-Box Based on 4D-4Wing Hyperchaotic System,” 3D Res., vol. 8, no. 1, pp. 1–9, Mar. 2017, doi: 10.1007/S13319-017-0119-X/METRICS.

[31] M. A. Arshed, S. Mumtaz, O. Riaz, W. Sharif, and S. Abdullah, “A Deep Learning Framework for Multi-Drug Side Effects Prediction with Drug Chemical Substructure,” Int. J. Innov. Sci. Technol., vol. 4, no. 1, pp. 19–31, 2022.

[32] M. T. Ubaid, M. Z. Khan, M. Rumaan, M. A. Arshed, M. U. G. Khan, and A. Darboe, “COVID-19 SOP’s Violations Detection in Terms of Face Mask Using Deep Learning,” 4th Int. Conf. Innov. Comput. ICIC 2021, 2021, doi: 10.1109/ICIC53490.2021.9692999.

[33] M. A. Arshed, H. Ghassan, M. Hussain, M. Hassan, A. Kanwal, and R. Fayyaz, “A Light Weight Deep Learning Model for Real World Plant Identification,” 2022 2nd Int. Conf. Distrib. Comput. High Perform. Comput. DCHPC 2022, pp. 40–45, 2022, doi: 10.1109/DCHPC55044.2022.9731841.

[34] H. Younis, M. A. Arshed, F. ul Hassan, M. Khurshid, and H. Ghassan, “Tomato Disease Classification using Fine-Tuned Convolutional Neural Network,” Int. J. Innov. Sci. Technol., vol. 4, no. 1, pp. 123–134, 2022, doi: 10.33411/ijist/2022040109.

[35] M. Mubeen, M. A. Arshed, and H. A. Rehman, “DeepFireNet - A Light-Weight Neural Network for Fire-Smoke Detection,” Commun. Comput. Inf. Sci., vol. 1616 CCIS, pp. 171–181, 2022, doi: 10.1007/978-3-031-10525-8_14/COVER.

[36] M. A. Arshed, S. Mumtaz, M. Hussain, R. Alamdar, M. T. Hassan, and M. Tanveer, “DeepFinancial Model for Exchange Rate Impacts Prediction of Political and Financial Statements,” 3rd IEEE Int. Conf. Artif. Intell. ICAI 2023, pp. 13–19, 2023, doi: 10.1109/ICAI58407.2023.10136658.

[37] R. A. A. Shahzad, M. A. Arshed, F. Liaquat, M. Tanveer, M. Hussain, “Pneumonia Classification from Chest X-ray Images Using Pre-Trained Network Architectures,” VAWKUM trans. Comput. sci., vol. 10, no. 2, pp. 34–44, 2022.

[38] M. T. M. A. Arshed, A. Shahzad, K. Arshad, D. Karim, S. Mumtaz, “Multiclass Brain Tumor Classification from MRI Images using Pre-Trained CNN Model,” VFAST trans. softw. eng., vol. 10, no. 4, pp. 22–28, 2022.

[39] M. A. Arshed et al., “Machine Learning with Data Balancing Technique for IoT Attack and Anomalies Detection,” Int. J. Innov. Sci. Technol., vol. 4, no. 2, pp. 490–498, 2022, doi: 10.33411/ijist/2022040218.

[40] H. A. Arshad, M. Hussain, A. Amin, and M. A. Arshed, “Impact of Artificial Intelligence in COVID-19 Pandemic: A Comprehensive Review,” 2022 2nd Int. Conf. Distrib. Comput. High Perform. Comput. DCHPC 2022, pp. 66–73, 2022, doi: 10.1109/DCHPC55044.2022.9732091.

[41] M. A. Arshed, W. Qureshi, M. Rumaan, M. T. Ubaid, A. Qudoos, and M. U. G. Khan, “Comparison of Machine Learning Classifiers for Breast Cancer Diagnosis,” 4th Int. Conf. Innov. Comput. ICIC 2021, 2021, doi: 10.1109/ICIC53490.2021.9692926.

[42] M. A. Arshed and F. Riaz, “Machine Learning for High Risk Cardiovascular Patient Identification 1,” J. Distrib. Comput. Syst., vol. 4, no. 2, pp. 34–39, 2021, Accessed: Dec. 26, 2023. [Online]. Available: https://ijdcs.ir/wp-content/uploads/2022/08/IJDCS-8-6.pdf

[43] M. Hussain, A. Shahzad, F. Liaquat, M. A. Arshed, S. Mansoor, and Z. Akram, “Performance Analysis of Machine Learning Algorithms for Early Prognosis of Cardiac Vascular Disease,” Tech. J., vol. 28, no. 02, pp. 31–41, Jun. 2023, Accessed: Dec. 26, 2023. [Online]. Available: https://tj.uettaxila.edu.pk/index.php/technical-journal/article/view/1778

[44] M. F. Idris, J. Sen Teh, J. L. S. Yan, and W. Z. Yeoh, “A Deep Learning Approach for Active S-Box Prediction of Lightweight Generalized Feistel Block Ciphers,” IEEE Access, vol. 9, pp. 104205–104216, 2021, doi: 10.1109/ACCESS.2021.3099802.

[45] G. Kim, H. Kim, Y. Heo, Y. Jeon, and J. Kim, “Generating Cryptographic S-Boxes Using the Reinforcement Learning,” IEEE Access, vol. 9, pp. 83092–83104, 2021, doi: 10.1109/ACCESS.2021.3085861.

Research Article

International Journal of Innovations in Science & Technology