Lossy Image Compression Unveiled: A Comprehensive Evaluation of DCT, Wavelet Transform, 
and Vector Quantization

Umer Ijaz; Muhammad Fraz Anwar; Abubaker Ijaz; Muhammad Hamza Kharal; Ammar Afzal; Ali Iqbal; Fouzia Gillani

Lossy Image Compression Unveiled: A Comprehensive Evaluation of DCT, Wavelet Transform, and Vector Quantization

Ijaz. U¹, Anwar. M. F¹, Ijaz. A², Kharal. M. H³, Afzal. A¹, Iqbal. A¹, Gillani. F⁴

¹ Department of Electrical Engineering & Technology, Government College University, Faisalabad, Pakistan

² WASA, Faisalabad, Pakistan

³ Department of Computer Science, Government College University, Faisalabad, Pakistan

⁴ Department of Mechanical Engineering & Technology, Government College University, Faisalabad, Pakistan

Abstract
The increasing demand for efficient image storage and transmission has driven extensive research into lossy image compression algorithms. This paper presents a comprehensive comparative analysis of three prominent lossy image compression techniques: Discrete Cosine Transform (DCT), Wavelet Transform, and Vector Quantization (VQ). Employing a diverse dataset and assessing their performance through key metrics, including Peak Signal-to-Noise Ratio (PSNR), Structural Similarity Index (SSIM), Mean Squared Error (MSE), Bitrate, and Computational Complexity, we meticulously evaluated these techniques across dimensions of image quality, compression efficiency, and computational demands. DCT emerges as a standout performer in preserving image quality, closely followed by Wavelet Transform. While Vector Quantization demonstrates efficiency in compression, its limitations become apparent in the realm of image quality preservation. The comparative analysis unequivocally positions DCT as the optimal choice for applications prioritizing image quality. This preference is substantiated by its remarkable PSNR and SSIM scores. Despite DCT not being the most computationally efficient, its ability to strike a crucial balance between compression efficiency and image quality renders it a well-rounded and effective solution. In conclusion, this research provides valuable insights into the comparative performance of DCT, Wavelet Transform, and VQ in the context of lossy image compression. The findings underscore DCT's superiority in image quality preservation, offering practical guidance for decision-makers in the field. The paper contributes to informed choices based on specific application requirements and emphasizes the pivotal role of DCT as a well-rounded and effective solution.

Keywords: Lossy Image Compression, Discrete Cosine Transform, Wavelet Transform, Vector Quantization, Image fidelity, Data Collection, Performance Metrics.

Corresponding Author	How to Cite this Article
Umer Ijaz, Department of Electrical Engineering & Technology, Government College University, Faisalabad, Pakistan	Umer Ijaz, Muhammad Fraz Anwar, Abubaker Ijaz, Muhammad Hamza Kharal, Ammar Afzal, Ali Iqbal, Fouzia Gillani, Lossy Image Compression Unveiled: A Comprehensive Evaluation of DCT, Wavelet Transform, and Vector Quantization . IJIST. 2023 ;5(4):847-861 https://journal.50sea.com/index.php/IJIST/article/view/600

Introduction

In the realm of modern digital imagery, the efficient storage and transmission of images have emerged as paramount considerations. Lossy image compression, a pivotal technique, holds the promise of addressing these challenges by significantly reducing the data size of images while striking a delicate balance between storage efficiency and perceptual image quality. With the ever-increasing demand for multimedia content and the proliferation of digital platforms, lossy compression algorithms play a crucial role in optimizing data transfer rates, conserving storage space, and enhancing user experiences. Lossy image compression [1] enables us to harness greater efficiency while preserving the essence of the original image. Lossy image compression [2] has a pivotal role in achieving enhanced data efficiency and economy in modern communications. Lossy image compression [3] helps in optimizing data handling, facilitating seamless storage, transmission, and download of images from the internet. Lossy Image compression algorithms [4], primarily intended for multimedia applications, have limited applicability in the medical image domain. In these cases, precision and information preservation are paramount. Lossy image compression [5] opens exciting possibilities for achieving versatile and high-quality image compression across a wide range of bitrates. This literature review offers valuable insights into advancements in image compression algorithms.

These results strongly validate our examination of three prevalent lossy image compression algorithms: Discrete Cosine Transform (DCT), Wavelet Transform, and Vector Quantization (VQ). Our evaluation encompasses compression efficacy, visual fidelity, and distortion reduction for these algorithms. The insights gained from this review provide a robust foundation for subsequent sections, focusing on the detailed comparison of DCT, Wavelet Transform, and VQ.

Objectives:

This research paper aims to achieve the following pivotal objectives:

• Undertake an exhaustive comparative analysis of three major lossy image compression algorithms—DCT, Wavelet Transform, and VQ.

• Assess the performance of these algorithms concerning image quality preservation, compression efficiency, and computational demands.

• Employ a varied array of evaluation metrics, encompassing Peak Signal-to-Noise Ratio (PSNR), Structural Similarity Index (SSIM), Mean Squared Error (MSE), Bit Rate, and Computational Complexity, to holistically evaluate the algorithms from diverse perspectives.

• Dataset Diversity: To utilize a diverse dataset containing images of different sizes, colors, and complexities to ensure the applicability and relevance of the findings to real-world scenarios.

• Practical Guidance: To provide practical insights and recommendations for decision-makers in the field of image compression, helping them make informed choices based on specific application requirements and trade-offs.

• Highlighting the Best Technique: To identify and recommend the most appropriate image compression technique, with the conclusion that the DCT excels in applications prioritizing image quality preservation.

These inferred objectives reflect the research paper's focus on comparing image compression techniques, assessing their performance using various metrics, and offering practical guidance for selecting the most suitable technique based on specific needs.

Novelty Statement and Justification:

This research paper stands out by conducting a thoroughly comprehensive overview of three major lossy image compression algorithms—DCT, Wavelet Transform, and VQ—setting itself apart from previous studies that typically concentrated on individual techniques. Notably, the paper employs a diverse dataset featuring images of various sizes, colors, and complexities, strengthening the relevance of its results in real-world applications. Embracing a comprehensive strategy, the research utilizes multiple assessment criteria, including PSNR, SSIM, MSE, Bit Rate, and Computational Complexity, providing in-depth insights into the effectiveness of the algorithms across various dimensions. Beyond a purely technical study, the paper offers practical insights, delving into trade-offs between image quality, compression efficiency, and processing demands—addressing the needs of decision-makers in the field. The research distinctly recommends DCT as the optimal technique for applications prioritizing image quality preservation, backed by extensive comparative analysis and practical considerations.

Literature Review:

As technology progresses, communication networks experience growing demands. Despite increased bandwidth, the rise in pixel and gray-level resolution from sensor and digital image technology poses a challenge. This is where image compression becomes a crucial research focus. Image compression [6] aims to reduce the necessary bits for image representation while maintaining its original quality. It's comparable to reducing the size of a large puzzle piece without compromising vital details. Refer to Figure 1 for an overview of the typical image compression process.

Figure 1: Procedure of Image Compression [7]

Figure 2: Illustrates images acquired using the application of the Lossy Compression Technique [11]

Compression reduces the data required for digital image representation by removing surplus or redundant bits. Key forms of redundancy include Coding redundancy, which involves the use of extra bits and underutilized code words; spatial and temporal redundancies (Interpixel Redundancy), resulting from correlations between adjacent pixels, leading to unnecessary duplication of information among connected pixels and irrelevant data, also known as Psychovisual Redundancy, where the human visual system disregards visually insignificant information. Over time, various image compression methods have emerged, broadly categorized into two core types: Lossy Compression and Lossless Compression [8].

Lossless compression processes each pixel individually, retaining every bit of the original data even after decompression. This results in reconstructed images that match the original numerically, ensuring full information restoration. Lossless compression achieves moderate compression levels while preserving data integrity [8]. Lossless image compression [9] methods achieve compression by eliminating redundancy within the image data.

Lossy image compression [10] strikes a delicate balance between maintaining image quality and introducing a controlled level of data loss. Refer to Figure (2) for a visual depiction of an image before and after undergoing the Lossy Compression Technique.

This research paper assessed the effectiveness of the following lossy compression algorithms:

Discrete Cosine Transform (DCT):

The DCT is a mathematical technique used to analyze and represent signals in a compact and efficient manner. The DCT is a pivotal technique with wide-ranging applications in fields such as image and video compression, audio processing, and data analysis. Its unique capability to convert spatial or temporal data into the frequency domain has brought about a change in basic assumptions in the storage and transmission of multimedia content, rendering it an indispensable tool in contemporary technology. The procedural stages of the DCT algorithm's operation are demonstrated in Figure 3.

Figure 3: Procedural stages of the DCT Algorithm’s Operation

DCT [12] introduces optimized matrix multiplication and quantization techniques. DCT reveals a significant increase in the compression ratio with minimal discernible alteration to the images, ensuring that the compressed images remain visually faithful to the original. DCT [13] reduces the data volume of high-resolution multimedia content while maintaining image quality at near-lossless standards. DCT [14] is a critical technology in today's digitally networked environment. It facilitates the smooth exchange of photographs and multimedia material, allowing files to be sent even under difficult network conditions while maintaining image quality. DCT is a pivotal component [15] in the compression algorithms evaluated in this study. It serves as the transformation step that plays a vital role in achieving compression by representing the data in the frequency domain. DCT facilitated [16] by a sensing matrix, isolates essential coefficients with lower dimensionality compared to the image's original dimensions.

Wavelet Transform:

Wavelet Transform is a potent signal processing method that uncovers both timing and frequency aspects in signals. The procedural stages of the Wavelet Transform algorithm's operation are demonstrated in Figure 4.

Wavelet Transform holds immense value in image processing, data compression, and biomedical signal analysis [17]. Operating with adaptable waves known as wavelets, it provides insights into frequency and spatial characteristics while preserving timing details. These wavelets are crafted from fundamental functions called mother wavelets. In this section, we will delve into how wavelet transformation benefits image watermarking and why it outshines other methods [18]. Wavelet Transform [19] stands as a key player in the landscape of image compression, offering a comprehensive solution to the challenges of constrained bandwidth and limited storage capacity. Wavelet Transform [20] a pivotal component of image information technology, has emerged as a crucial tool in the pursuit of lossy image compression while maintaining the desired quality. Recent research highlights the efficacy of a two-step method, offering both simplicity and reduced compression time, all while ensuring the accuracy of visual quality. Wavelet Transform [21] is a cornerstone in the landscape of image compression if we compare it with contemporary techniques within the realm of lossy image compression. Wavelet Transform [22] is a potent tool for low-bit-rate image compression.

Figure 4: Procedural Stages of the Wavelet Transform Algorithm’s Operation

Vector Quantization (VQ):

VQ is a versatile and powerful technique employed in data compression, pattern recognition, and signal processing. VQ is a highly regarded asset in today's research and engineering landscape. It shines particularly in handling the escalating complexity and sheer volume of data. Its ability to balance compression efficiency with data representation quality makes it an indispensable component of various technologies and systems. The procedural stages of the VQ algorithm's operation are demonstrated in Figure 5.

VQ [24] is an important multimedia technique that ensures effective image and audio compression. By compactly representing information, VQ strikes a balance between cost efficiency and data quality, offering a powerful solution for a wide range of signal types. VQ [25] is a core technology in digital image processing, with a particular emphasis on image compression. VQ [26] is crucial to novel image coding algorithms. VQ [23] is a cutting-edge technique for lossy image compression, a crucial aspect of image data management in fields such as multimedia and medical diagnosis. The demand for efficient storage and data transmission of digital images, particularly in the medical domain, where images play a pivotal role in diagnosis, underscores the significance of advanced compression methods. All these make VQ an ideal choice for use in those digital image compression applications.

Material and Method

The approach used to compare the performance of the chosen image compression algorithms, namely DCT, Wavelet Transform, and VQ, followed a systematic method to assess their effectiveness. The study was conducted using MATLAB programming language, taking advantage of relevant libraries to implement the algorithms effectively.

Figure 5: Procedural stages of the VQ Algorithm’s Operation

Data Acquisition and Preparation:

The dataset component of the research report examined Image Compression Algorithms using a variety of pictures [27]. The dataset comprised photos of various items and locations, with image size, colors, and complexity considered. The image sizes ranged from 256x256 to 1024x1024 pixels. Some exhibited a lot of detail while using 24-bit colors, while others had less detail when using 8-bit colors. This combination allows us to observe how effectively the algorithms operate with different hues. The collection also included two sorts of colors: black and white photographs and images with colors such as red, green, and blue. This dataset lets us carefully assess the chosen image compression algorithms in many real-life situations. This helps us understand how well the algorithms work with diverse kinds of images and complexities.

Performance Metrics and Evaluation Criteria:

In assessing each algorithm's performance, key parameters such as Bit Rate, PSNR, SSIM, MSE, and Computational Complexity were meticulously evaluated.

Bit Rate:

Bit Rate denotes the average bit count required for a single pixel representation in a compressed image. Lower bit rates signify more efficient compression, reducing storage needs and accelerating data transmission. Determining the optimal bit rate hinges on the application and user preferences, striking a balance between image quality and file size. Higher bit rates are conducive to high-quality applications, while lower bit rates are preferable in bandwidth-limited scenarios [28][29][30][31][32].

Computational Complexity: Computational Complexity assesses the resources required for compression, influencing processing time. Reduced computational complexity enables swift compression and decompression, rendering an algorithm well-suited for real-time applications and resource-constrained devices. The optimal range depends on available hardware and real-time processing requirements [33][34][35][36][37].

Mean Square Error:

MSE quantifies the average squared difference between original and compressed images. Lower MSE values indicate enhanced image quality, although its sensitivity to outliers may not precisely mirror perceived quality. The optimal range fluctuates based on desired image quality, with extremely low MSE favored for high-quality images [38][39][40][41][42].

Peak Signal-to-Noise Ratio:

PSNR evaluates how accurately a compressed image replicates the original, with higher values denoting superior image quality. PSNR values above 30 are generally suitable, surpassing 40 in high-quality scenarios such as medical imaging [43][44][45][46][47].

Structural Similarity Index:

SSIM evaluates structural resemblance between original and compressed images, considering luminance, contrast, and structure. SSIM values exceeding 0.9 are considered optimum for image quality, reflecting human perception better than MSE and PSNR [48][49][50][51][52].

PSNR and SSIM gauge image quality, while MSE measures image similarity. Compression Ratio compares the sizes of original and compressed images, and Computational Complexity scales with image size. The assessment, performed on five test images, yielded average results for each algorithm, enabling a thorough performance comparison through line graphs.

Algorithm Implementation and Execution:

The implementation of image compression involves a systematic process outlined below. The code encompasses three distinct algorithms: Discrete Cosine Transform (DCT), Wavelet Transform, and Vector Quantization (VQ). These algorithms are evaluated based on various metrics such as PSNR, SSIM, MSE, RMSE, Compression Ratio, Bit Rate, and Computational Complexity. The sequential steps of lossy image compression algorithms implementation and execution are demonstrated in Figure 6.

Figure 6: Sequential Steps Involving Lossy Image Compression Algorithms Implementation

In this comprehensive image compression and evaluation workflow, the sequential steps ensure a structured and thorough analysis. The process begins with the initialization and specification of essential input parameters, including clearing existing data and defining image file names. The algorithm seamlessly reads, processes, and evaluates each specified image utilizing lossy image compression techniques such as Discrete Cosine Transform (DCT), Wavelet, and Vector Quantization (VQ). Crucial metrics such as PSNR, SSIM, MSE, RMSE, Bit Rate, and Computational Complexity are meticulously recorded. Following the evaluations, the results are aggregated and averaged across all images for each algorithm, providing an effective comparison. To ensure the preservation of valuable findings, the evaluation results, encompassing a range of metrics and image-specific details, are saved in a MAT file. This meticulous workflow enables a comprehensive exploration of image compression algorithms, facilitating informed decision-making and insights into their relative performance.

Result and Discussion

Results and Comparative Analysis:

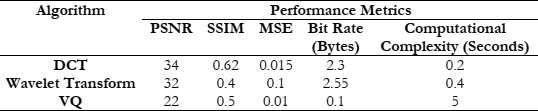
Experimental outcomes demonstrate how well DCT, Wavelet Transform, and Vector Quantization perform based on the metrics mentioned. The scores for PSNR and SSIM show how well the image quality is maintained, where higher scores mean better results. On the other hand, the values of MSE and RMSE indicate the size of errors, with lower values being more favorable. The bitrate indicates how much compression each algorithm achieves. Additionally, the computational complexity highlights the efficiency of the algorithms in terms of processing speed and resource consumption.

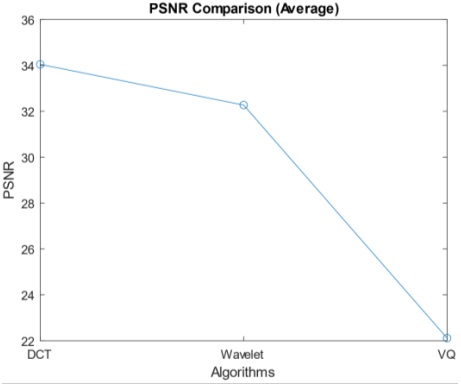
The PSNR Comparison Graph (Figure 7) is a vital tool for assessing the effectiveness of various image compression algorithms. With PSNR values on the y-axis, a critical metric for measuring compressed image quality against the original, and the x-axis featuring the considered algorithms, higher PSNR values signify enhanced compressed image quality and minimized distortion. The comparative analysis reveals distinctive PSNR values for three algorithms. The DCT algorithm excels with a notable PSNR of 34, signifying high image quality preservation during compression. Renowned for its efficiency in transforming images into the frequency domain, DCT stands out as a robust choice. Wavelet Transform, with a PSNR of 32, also showcases commendable performance in preserving image quality, particularly excelling at retaining details, though slightly trailing DCT in PSNR. In contrast, VQ, with a PSNR of 22, notably lags in image quality preservation compared to the other algorithms. This lower PSNR score implies more visible distortion and diminished image fidelity in the compressed results. The comparative analysis, based on PSNR values, underscores the superiority of DCT in maintaining image quality, closely followed by Wavelet Transform. VQ significantly falls behind in this aspect. When selecting an image compression technique, it is imperative to consider your application's specific needs and strike an appropriate balance between compression efficiency and image quality.

Figure 7: Comparison Graph of PSNR

Figure 8: Comparison Graph of SSIM

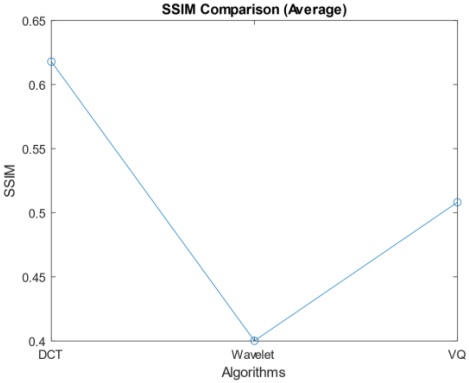
The SSIM Comparison Graph (Figure 8) is instrumental in assessing the effectiveness of various image compression methods. SSIM values, a critical measure of the fidelity of compressed images to the original, are depicted on the y-axis, while the x-axis showcases the evaluated algorithms. Higher SSIM values signify greater similarity and, consequently, better preservation of image quality. Upon analyzing the results, distinct SSIM values emerge for three image compression algorithms. DCT achieves a robust SSIM score of 0.62, indicating a high level of structural similarity between the compressed and original images. This underscores DCT's effectiveness in retaining the structural intricacies of images during compression. Wavelet Transform, with an SSIM score of 0.4, also demonstrates commendable performance in terms of structural similarity, although it slightly trails DCT. Vector Quantization exhibits an SSIM of 0.5, indicating moderate structural similarity but not performing as well as DCT in preserving image structure. Comparative analysis based on SSIM values highlights DCT's excellence in retaining the structural integrity of images, followed by VQ. While effective, Wavelet Transform lags slightly in this aspect. When selecting an image compression method, it is crucial to consider the specific application requirements and strike the desired balance between compression efficiency and structural image quality.

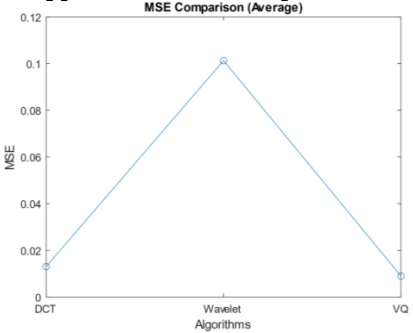
The MSE Comparison Graph (Figure 9) provides essential insights into the effectiveness of diverse image compression algorithms. Displaying MSE values on the y-axis, a crucial metric for assessing the quality of compressed images, lower MSE values indicate enhanced image quality and a closer resemblance between the compressed and original images. On the x-axis, various algorithms are evaluated, revealing distinct outcomes. DCT stands out with an impressively low MSE of 0.015, indicating that DCT-based compression produces compressed images closely resembling the original, resulting in minimal distortion. Wavelet Transform exhibits a higher MSE of 0.1, implying a proficient level of image quality preservation but with slightly more distortion, remaining visually acceptable. VQ registers an MSE of 0.01, on par with DCT, signifying that VQ-based compression also maintains an elevated level of image quality with minimal distortion. Comparative analysis based on MSE values reveals that both DCT and VQ excel in preserving image quality. While Wavelet Transform is acceptable, it introduces slightly more distortion. When selecting an image compression method, it is crucial to consider specific application needs and prioritize the importance of preserving image quality.

Figure 9: Comparison Graph of MSE

Figure 10: Bitrate comparison graph

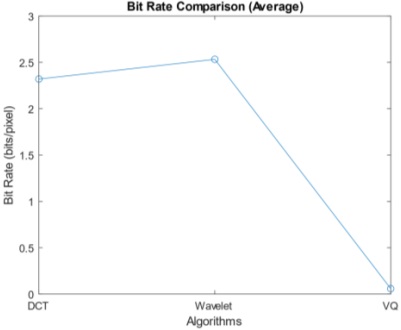
The Bit Rate comparison graph (Figure 10) offers vital insights into the efficacy of various image compression methods. The bit rate values are depicted on the y-axis, while the x-axis enumerates the algorithms under evaluation. Let us delve into the findings and make a comparative assessment. DCT-based image compression operates at a bit rate of 2.3, meaning it requires approximately 2.3 bits for each pixel in the compressed image. This equilibrium effectively balances compression efficiency and image quality. In contrast, Wavelet Transform-based compression operates less efficiently, with a bit rate of 2.55, requiring approximately 2.55 bits per pixel in the compressed image. Although this indicates a slightly higher bit rate compared to DCT, it may still be suitable for specific application needs. On the efficiency front, Vector Quantization-based compression excels with an impressively low bit rate of only 0.1. This implies that VQ-based methods use significantly fewer bits per pixel, making them highly efficient for compression. However, this efficiency may come at the cost of some image quality. DCT strikes a balanced middle ground between compression efficiency and image quality. Wavelet Transform is slightly less efficient but still reasonable for many applications. On the other hand, Vector Quantization stands out as extremely efficient but may result in some loss of image quality. The selection of the most suitable algorithm should align with the specific needs of the image compression task at hand, considering factors such as image quality requirements and available bandwidth or storage constraints.

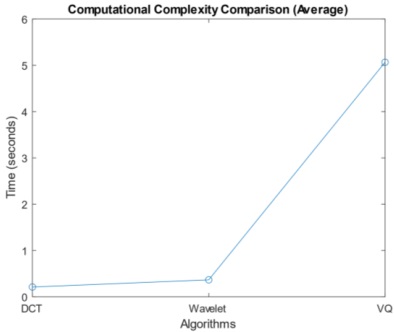
Figure 11: Comparison graph of Computational Complexity

The Computational Complexity Comparison graph (Figure 11) is instrumental in evaluating the computational demands of various image compression algorithms. Representing Computational Complexity in seconds on the y-axis and listing the algorithms on the x-axis, we can now conduct a comparative analysis using the obtained results. DCT-based image compression exhibits a low computational complexity of 0.2 seconds. This means that DCT-based methods can process an image with reasonable speed, making them suitable for real-time or time-sensitive applications. Wavelet Transform-based compression, while more computationally intensive than DCT, still maintains an acceptable level of efficiency with a complexity of 0.4 seconds. It may be slightly slower than DCT but is well-suited for applications where computational speed is not the sole priority. Among the considered algorithms, VQ exhibits the highest computational complexity, taking 5 seconds to compress an image. This signifies that VQ-based methods demand more computational resources and time. They are better suited for scenarios prioritizing compression efficiency over computational speed. When making a comparative analysis and choosing an image compression algorithm, careful consideration of the application's specific requirements is essential. DCT strikes a favorable balance between computational efficiency and compression quality. While slightly slower, Wavelet Transform remains reasonable for most applications. VQ, with its higher computational complexity, shines in situations where compression efficiency takes precedence and computational resources are not constrained.

Table 1: Comprehensive Table encompassing values of DCT, Wavelet Transform, and VQ

Table 1 presents a comprehensive overview of DCT, Wavelet Transform, and Vector Quantization values. The DCT algorithm stands out with a high PSNR, indicating minimal image quality loss. Its robust SSIM score signifies strong structural similarity, and the exceptionally low MSE reflects accurate pixel value prediction. With a low bit rate, DCT strikes a balance for compression, coupled with efficient computational complexity for real-time applications. The Wavelet Transform algorithm offers good image quality, though with a slightly lower SSIM than DCT. The moderate MSE value and slightly higher bit rate suggest a trade-off for improved image quality. While its computational complexity is slightly higher than DCT, it suits applications requiring a balance between compression and speed. Vector Quantization records the lowest PSNR, indicating notable image quality loss, but with a moderate SSIM and commendably low MSE, implying accurate pixel prediction. Efficient in bit rate, Vector Quantization prioritizes substantial compression. However, its high computational complexity makes it suitable for scenarios prioritizing compression efficiency over speed.

Discussion:

Interpretation of Findings:

The findings of our comparative analysis shed light on the distinct strengths and weaknesses of three major lossy image compression algorithms: DCT, Wavelet Transform, and VQ. DCT stands out as the clear winner in preserving image quality, evident from its high PSNR and SSIM scores. Its efficient transformation of images into the frequency domain contributes to superior image fidelity. Wavelet Transform closely follows, excelling in scenarios where a compromise between image quality and compression efficiency is acceptable. Its versatility in capturing both frequency and spatial information makes it a compelling choice. However, VQ, while showcasing commendable compression efficiency, lags significantly behind in terms of image quality preservation.

Implications for Practical Applications:

The practical implications of our research are substantial, offering guidance for decision-makers in the field of image compression. DCT emerges as the optimal choice for applications prioritizing image quality preservation. Its balance between compression efficiency and image fidelity makes it a well-rounded solution, particularly suitable for scenarios where maintaining the essence of the original image is paramount. Wavelet Transform, while slightly trailing DCT, proves valuable in situations where a nuanced compromise between image quality and compression efficiency is acceptable. VQ, with its impressive compression efficiency, is most suited for scenarios prioritizing substantial compression ratios over strict image quality requirements.

Trade-offs and Considerations:

In navigating the landscape of lossy image compression, trade-offs become inevitable. DCT, while excelling in image quality preservation, is not the most computationally efficient. This may pose challenges in real-time applications where swift processing is critical. Wavelet Transform, offering a balance between image quality and compression efficiency, might be a preferred choice for applications where computational speed is not the sole priority. On the other hand, VQ's exceptional compression efficiency comes at the cost of notable image quality loss, making it suitable for scenarios where substantial compression ratios outweigh stringent image quality demands.

Conclusion

In the digital age, efficient image compression is vital for storage, transmission, and user experiences. Our analysis of three top lossy image compression methods — DCT, Wavelet Transform, and VQ — provides key insights into their strengths and weaknesses. DCT stands out for applications prioritizing image quality preservation. It boasts high PSNR and SSIM scores, indicating superior image fidelity. Although not the most computationally efficient, DCT strikes a balance between compression efficiency and image quality. Wavelet Transform, while slightly behind DCT in image quality preservation, excels when compromise is acceptable. It captures both frequency and spatial information, making it versatile. VQ shines in compression efficiency, demanding minimal bits per pixel. However, it sacrifices image quality with lower PSNR and SSIM scores. It is ideal for scenarios needing high compression ratios where some loss of image quality is acceptable. After conducting a thorough comparative analysis of three leading lossy image compression algorithms, the DCT unequivocally stands out as the optimal technique, especially for applications prioritizing image quality preservation. DCT excels with its high PSNR and SSIM scores, demonstrating unparalleled image fidelity. Despite not being the most computationally efficient, DCT successfully achieves a crucial balance between compression efficiency and image quality, solidifying its unequivocal preference for such applications.

Acknowledgement:

The authors are thankful to the “Government College University Faisalabad” and “Water and Sanitation Agency Faisalabad (WASA-FDA)” for providing lab support to conduct the research work.

Reference

[1] Marlapalli, K., Bandlamudi, R.S., Busi, R., Pranav, V. and Madhavrao, B., 2020. A review on image compression techniques. Communication Software and Networks: Proceedings of INDIA 2019, pp.271-279.

[2] Al-jawaherry, M.A. and Hamid, S.Y., 2021. Image Compression techniques: literature review. Journal of Al-Qadisiyah for computer science and mathematics, 13(4), pp. Page-10.

[3] Shah, T.J. and Banday, M.T., 2020. A review of contemporary image compression techniques and standards. Examining Fractal Image Processing and Analysis, pp.121-157.

[4] Patidar, G., Kumar, S. and Kumar, D., 2020, February. A review on medical image data compression techniques. In 2nd International Conference on Data, Engineering and Applications (IDEA) (pp. 1-6). IEEE.

[5] Helminger, L., Djelouah, A., Gross, M. and Schroers, C., 2020. Lossy image compression with normalizing flows. arXiv preprint arXiv:2008.10486.

[6] Marlapalli, K., Bandlamudi, R.S.B.P., Busi, R., Pranav, V., Madhavrao, B. (2021). A Review of Image Compression Techniques. In: Satapathy, S.C., Bhateja, V., Ramakrishna Murty, M., Gia Nhu, N., Jayasri Kotti (eds) Communication Software and Networks. Lecture Notes in Networks and Systems, vol 134. Springer, Singapore. https://doi.org/10.1007/978-981-15-5397-4_29.

[7] Rahman, M.A. and Hamada, M., 2019. Lossless image compression techniques: A state-of-the-art survey. Symmetry, 11(10), p.1274.

[8] S. P. Amandeep Kaur, Sonali Gupta, Lofty Sahi, “COMPREHENSIVE STUDY OF IMAGE COMPRESSION TECHNIQUES,” J. Crit. Rev., vol. 7, no. 17, pp. 2382–2388, 2020.

[9] Rahman, A., Hamada, M. and Rahman, A., 2022. A comparative analysis of the state-of-the-art lossless image compression techniques. In SHS Web of Conferences (Vol. 139, p. 03001). EDP Sciences.

[10] Prasanna, Y.L., Tarakaram, Y., Mounika, Y. and Subramani, R., 2021, September. Comparison of different lossy image compression techniques. In 2021 International Conference on Innovative Computing, Intelligent Communication and Smart Electrical Systems (ICSES) (pp. 1-7). IEEE.

[11] Al-jawaherry, M.A. and Hamid, S.Y., 2021. Image Compression techniques: literature review. Journal of Al-Qadisiyah for computer science and mathematics, 13(4), pp. Page-10.

[12] Shawahna, A., Haque, M.E. and Amin, A., 2019. JPEG image compression using the discrete cosine transform: an overview, applications, and hardware implementation. arXiv preprint arXiv:1912.10789.

[13] Agarwal, M., Gupta, V., Goel, A. and Dhiman, N., 2022, November. Near lossless image compression using discrete cosine transformation and principal component analysis. In AIP Conference Proceedings (Vol. 2481, No. 1). AIP Publishing.

[14] John, J., 2021. Discrete cosine transform in JPEG compression. arXiv preprint arXiv:2102.06968.

[15] Pinto, A.C., Maciel, M.D., Pinho, M.S., Medeiros, R.R. and Moraes, A.O., 2022. Evaluation of lossy compression algorithms using discrete cosine transform for sounding rocket vibration data. Measurement Science and Technology, 34(1), p.015117.

[16] Ashour, A.S., Guo, Y., Alaa, E.E. and Kasem, H.M., 2020. Discrete cosine transform–based compressive sensing recovery strategies in medical imaging. In Advances in Computational Techniques for Biomedical Image Analysis (pp. 167-184). Academic Press.

[17] Muthukrishnan, A. Kumar, D. V., and Kanagaraj M. (2019). Internet of image things-discrete wavelet transform, and Gabor wavelet transform based image enhancement resolution technique for IoT satellite applications. Cognitive Systems Research, vol. 57, pp. 46-53.

[18] Zebari, D. A., Zeebaree, D. Q., Saeed, J. N., Zebari, N. A., & Adel, A. Z. (2020). Image Steganography Based on Swarm Intelligence Algorithms: A Survey.people,7(8), 9.

[19] Annalakshmi, N., 2021. Lossy image compression techniques. Int J Comput Appl, 183, pp.30-34.

[20] Li, F., Krivenko, S. and Lukin, V., 2020. Two-step providing of desired quality in lossy image compression by SPIHT. Radioelectronic and computer systems, (2), pp.22-32.

[21] Thakker, A., Namboodiri, N., Mody, R., Tasgaonkar, R. and Kambli, M., 2022, December. Lossy Image Compression-A Comparison Between Wavelet Transform, Principal Component Analysis, K-Means and Autoencoders. In 2022 5th International Conference on Advances in Science and Technology (ICAST) (pp. 569-576). IEEE.

[22] Boujelbene, R., Boubchir, L. and Ben Jemaa, Y., 2019. Enhanced embedded zerotree wavelet algorithm for lossy image coding. IET Image Processing, 13(8), pp.1364-1374.

[23] Mohanta, G., and Mohanta, H.C., 2019. Image compression using different vector quantization algorithms and its comparison. IJITEE journal, 8(9).

[24] Adokar, D.U. and Gurjar, A.A., 2020. Image Compression using Vector Quantization. Grenze International Journal of Engineering & Technology (GIJET), 6(2).

[25] Purohit, V., 2023. Image Compression Using Wavelets and Vector Quantization Techniques. Applied Science and Engineering Journal for Advanced Research, 2(2), pp.14-18.

[26] Agrawal, S., 2020. Finite-State Vector Quantization Techniques for Image Compression. International Research Journal of Innovations in Engineering and Technology, 4(7), p.1.

[27] https://sipi.usc.edu/database/database.php?volume=misc

[28] Choi, H. and Bajić, I.V., 2022. Scalable image coding for humans and machines. IEEE Transactions on Image Processing, 31, pp.2739-2754.

[29] Le, N., Zhang, H., Cricri, F., Ghaznavi-Youvalari, R., Tavakoli, H.R. and Rahtu, E., 2021, July. Learned image coding for machines: A content-adaptive approach. In 2021 IEEE International Conference on Multimedia and Expo (ICME) (pp. 1-6). IEEE.

[30] Chen, T., Liu, H., Ma, Z., Shen, Q., Cao, X. and Wang, Y., 2021. End-to-end learnt image compression via non-local attention optimization and improved context modeling. IEEE Transactions on Image Processing, 30, pp.3179-3191.

[31] Yuan, F., Zhan, L., Pan, P. and Cheng, E., 2021. Low bit-rate compression of underwater image based on human visual system. Signal Processing: Image Communication, 91, p.116082.

[32] Cho, S., Lee, J., Kim, J., Kim, Y., Kim, D.W., Chung, J. and Jung, S., 2019, June. Low Bit-rate Image Compression based on Post-processing with Grouped Residual Dense Network. In CVPR Workshops (p. 0).

[33] Lin, A., Chen, B., Xu, J., Zhang, Z., Lu, G. and Zhang, D., 2022. Ds-transunet: Dual swin transformer u-net for medical image segmentation. IEEE Transactions on Instrumentation and Measurement, 71, pp.1-15.

[34] Wang, W., Chen, C., Ding, M., Yu, H., Zha, S. and Li, J., 2021. Transbts: Multimodal brain tumor segmentation using transformer. In Medical Image Computing and Computer Assisted Intervention–MICCAI 2021: 24th International Conference, Strasbourg, France, September 27–October 1, 2021, Proceedings, Part I 24 (pp. 109-119). Springer International Publishing.

[35] Zamir, S.W., Arora, A., Khan, S., Hayat, M., Khan, F.S. and Yang, M.H., 2022. Restormer: Efficient transformer for high-resolution image restoration. In Proceedings of the IEEE/CVF conference on computer vision and pattern recognition (pp. 5728-5739).

[36] Hatamizadeh, A., Tang, Y., Nath, V., Yang, D., Myronenko, A., Landman, B., Roth, H.R. and Xu, D., 2022. Unetr: Transformers for 3d medical image segmentation. In Proceedings of the IEEE/CVF winter conference on applications of computer vision (pp. 574-584).

[37] Valanarasu, J.M.J., Oza, P., Hacihaliloglu, I. and Patel, V.M., 2021. Medical transformer: Gated axial-attention for medical image segmentation. In Medical Image Computing and Computer Assisted Intervention–MICCAI 2021: 24th International Conference, Strasbourg, France, September 27–October 1, 2021, Proceedings, Part I 24 (pp. 36-46). Springer International Publishing.

[38] Chicco, D., Warrens, M.J. and Jurman, G., 2021. The coefficient of determination R-squared is more informative than SMAPE, MAE, MAPE, MSE and RMSE in regression analysis evaluation. PeerJ Computer Science, 7, p.e623.

[39] Singh, H., Ahmed, A.S., Melandsø, F. and Habib, A., 2023. Ultrasonic image denoising using machine learning in point contact excitation and detection method. Ultrasonics, 127, p.106834.

[40] Kumar, A. and Dua, M., 2023. Image encryption using a novel hybrid chaotic map and dynamic permutation− diffusion. Multimedia Tools and Applications, pp.1-24.

[41] Lu, Y., Gong, M., Cao, L., Gan, Z., Chai, X. and Li, A., 2023. Exploiting 3D fractal cube and chaos for effective multi-image compression and encryption. Journal of King Saud University-Computer and Information Sciences, 35(3), pp.37-58.

[42] Rashid, O., Amin, A. and Lone, M.R., 2020, December. Performance analysis of DWT families. In 2020 3rd International Conference on Intelligent Sustainable Systems (ICISS) (pp. 1457-1463). IEEE.

[43] Sara, U., Akter, M. and Uddin, M.S., 2019. Image quality assessment through FSIM, SSIM, MSE and PSNR—a comparative study. Journal of Computer and Communications, 7(3), pp.8-18.

[44] Huang, Y., Niu, B., Guan, H. and Zhang, S., 2019. Enhancing image watermarking with adaptive embedding parameter and PSNR guarantee. IEEE Transactions on Multimedia, 21(10), pp.2447-2460.

[45] Thanh, D.N.H. and Engínoğlu, S., 2019. An iterative mean filter for image denoising. IEEE Access, 7, pp.167847-167859.

[46] Elhadad, A., Ghareeb, A. and Abbas, S., 2021. A blind and high-capacity data hiding of DICOM medical images based on fuzzification concepts. Alexandria engineering journal, 60(2), pp.2471-2482.

[47] Chen, W., Qi, B., Liu, X., Li, H., Hao, X. and Peng, Y., 2022. Temperature‐Robust Learned Image Recovery for Shallow‐Designed Imaging Systems. Advanced Intelligent Systems, 4(10), p.2200149.

[48] Juan, W.Y., 2021. Generating Synthesized Computed Tomography (CT) from Magnetic Resonance Imaging Using Cycle-Consistent Generative Adversarial Network for Brain Tumor Radiation Therapy. International Journal of Radiation Oncology, Biology, Physics, 111(3), pp. e111-e112.

[49] Setiadi, D.R.I.M., 2021. PSNR vs SSIM: imperceptibility quality assessment for image steganography. Multimedia Tools and Applications, 80(6), pp.8423-8444.

[50] Nilsson, J. and Akenine-Möller, T., 2020. Understanding ssim. arXiv preprint arXiv:2006.13846.

[51] Starovoytov, V.V., Eldarova, E.E. and Iskakov, K.T., 2020. Comparative analysis of the SSIM index and the pearson coefficient as a criterion for image similarity. Eurasian journal of mathematical and computer applications, 8(1), pp.76-90.

[52] Peng, J., Shi, C., Laugeman, E., Hu, W., Zhang, Z., Mutic, S. and Cai, B., 2020. Implementation of the structural SIMilarity (SSIM) index as a quantitative evaluation tool for dose distribution error detection. Medical physics, 47(4), pp.1907-1919.

Research Article

International Journal of Innovations in Science & Technology