Fine-Tuning Audio Compression: Algorithmic Implementation and Performance Metrics

Umer Ijaz; Fouzia Gillani; Ali Iqbal; Muhammad Saad Sharif; Muhammad Fraz Anwar; Abubaker Ijaz

Fine-Tuning Audio Compression: Algorithmic Implementation and Performance Metrics

Ijaz. U¹, Gillani. F², Iqbal. A¹, Sharif. M. S¹, Anwar. M. F¹, Ijaz. A³

¹ Department of Electrical Engineering & Technology, Government College University, Faisalabad, Pakistan

² Department of Mechanical Engineering & Technology, Government College University, Faisalabad, Pakistan

³ WASA, Faisalabad, Pakistan

Abstract

Introduction/Importance of Study:

This study introduces a comprehensive evaluation of audio compression algorithms to address the increasing demand for efficient data compression techniques in various audio processing applications.

Novelty statement:

Our research contributes novel insights into the comparative analysis of audio compression algorithms, offering a systematic approach to assess performance across multiple dimensions.

Material and Method:

The research methodology involved the selection of a diverse dataset comprising five audio files, rigorous implementation of four prominent compression algorithms, and systematic evaluation of performance metrics.

Results and Discussion:

The abstract primarily focuses on presenting the findings of the comparative analysis, highlighting the performance of MP3, LPC, Wavelet, and Sub band algorithms across various evaluation parameters.

Concluding Remarks:

In conclusion, our study identifies Wavelet compression as the optimal choice among the evaluated algorithms, offering exceptional accuracy, perceptual quality, and minimal distortion in audio compression.

Keywords: Audio Compression, Algorithm Evaluation, MP3 Compression, LPC Compression, Wavelet Compression, Subband Compression, Performance Metrics, Comparative Study, Digital Signal Processing, Multimedia Applications.

Corresponding Author	How to Cite this Article
Umer Ijaz, Department of Electrical Engineering & Technology, Government College University, Faisalabad, Pakistan	Umer Ijaz, Fouzia Gillani, Ali Iqbal, Muhammad Saad Sharif, Muhammad Fraz Anwar, Abubaker Ijaz, Fine-Tuning Audio Compression: Algorithmic Implementation and Performance Metrics. IJIST. 2024 ;6(1):220-236 https://journal.50sea.com/index.php/IJIST/article/view/714

Introduction

Audio compression is a fundamental aspect of digital signal processing, pivotal for the efficient storage and transmission of multimedia content. As the demand for high-quality audio experiences grows, the choice of compression algorithms becomes increasingly critical. This paper embarks on a comprehensive exploration of four prominent audio compression techniques such as MP3, LPC, Wavelet, and Subband, aiming to provide a nuanced understanding of their comparative performance. Considering the exponential increase in digital audio consumption and the diversity of applications relying on efficient compression, an in-depth analysis of these algorithms is essential to inform practitioners and researchers in the field. Historically, audio compression algorithms [1] have struggled to strike a balance between preserving sound quality, achieving significant compression ratios, and facilitating real-time access. Early attempts often resulted in compromised audio fidelity and limited practicality for real-time applications. Consequently, the pursuit of audio compression has emerged as a critical research area and a lucrative business domain, driven by the imperative to store data with uncompromised quality while mitigating storage costs. In the realm of audio compression [2], the pursuit of optimal compression techniques intersects with the burgeoning field of emotion recognition, presenting a compelling avenue for exploration and innovation. In the era of burgeoning data volumes and the imperative for secure transmission, the development of audio compression systems [3] that concurrently ensure data security has emerged as a compelling avenue of research. The pressing need to optimize storage utilization, expedite data transmission, and safeguard sensitive signals over constrained and vulnerable communication channels underscores the significance of this research endeavor.

Consequently, researchers have dedicated significant efforts to devising diverse systems aimed at compressing or encrypting audio data, encountering challenges such as computational complexity and time consumption. The importance of this research lies in the need to identify the strengths and weaknesses of each algorithm, facilitating informed decision-making in real-world applications. While existing literature often highlights individual compression techniques, a comprehensive comparative study is notably absent. Our research aims to address this gap by providing a comprehensive evaluation of MP3, LPC, Wavelet, and Subband algorithms, thereby bridging the knowledge divide in audio compression. This comparative analysis not only serves to enhance our understanding of these techniques but also aids in identifying the most suitable algorithm for specific use cases, contributing to advancements in audio compression technologies. In the realm of existing technologies, there is a noticeable lack of studies providing a side-by-side assessment of multiple audio compression algorithms. While individual algorithmic performances have been extensively explored, a comprehensive comparative study is essential for a holistic perspective.

Objective:

This research endeavors to fill this gap by systematically evaluating the identified algorithms, shedding light on their relative strengths and weaknesses. The absence of such comparative analyses limits the ability of practitioners to make informed decisions about algorithm selection based on their unique requirements.

Problem Statement:

The problem statement at the core of this research revolves around the lack of a unified understanding of the comparative performance of MP3, LPC, Wavelet, and Subband compression algorithms. By addressing this gap, we aim to provide a comprehensive resource that assists practitioners and researchers in making informed decisions about the most suitable algorithm for specific applications.

Proposed Solution:

The proposed solution involves subjecting the algorithms to a standardized evaluation framework, encompassing metrics such as Mean Square Error (MSE), Root Mean Square Error (RMSE), Perceptual Evaluation of Speech Quality (PESQ), Spectral Similarity Index (SSI), and Total Harmonic Distortion (THD).

Primary Objective:

The primary objective of this research is to conduct an exhaustive comparative study of MP3, LPC, Wavelet, and Subband audio compression algorithms, systematically evaluating their performance across multiple metrics. This includes understanding how each algorithm preserves audio quality, manages compression artifacts, and responds to several types of audio content.

Novelty Statement:

A key novelty of this study lies in its comprehensive and comparative nature, offering a holistic view of multiple audio compression algorithms. By filling the gap in the understanding of comparative performance, the research provides valuable insights for practical implementation and algorithm optimization.

The research goes beyond isolated assessments by presenting a side-by-side comparison of MP3, LPC, Wavelet, and Subband techniques, facilitating a deeper understanding of their relative merits. The justification for this novelty is rooted in the practical need for a unified resource that aids practitioners and researchers in making well-informed decisions about audio compression algorithm selection based on their specific requirements.

The progression of discussions in the subsequent sections of this paper is as follows. The following sections of the research paper will explore the Literature Review (Section 2), thoroughly examining individual components, identifying research gaps, assessing the feasibility of addressing these gaps, and substantiating discussions with the latest citations and appropriately cited figures. In Section 3, the Material and Method are expounded, elucidating details about the audio files and metrics utilized for performance evaluation. Section 4 concentrates on Results and Comparative Analysis, providing an in-depth examination of the comparative performance of the MP3, LPC, Wavelet, and Subband algorithms. Discussion (Section 5) will interpret research findings, explore their implications for practical applications, and analyze tradeoffs and considerations associated with the study. Finally, Section 6 encapsulates conclusions drawn from the findings, summarizing key takeaways and their implications for practical applications.

Literature Review:

Integral to digital signal processing [4], audio compression serves as a cornerstone in enhancing the efficiency of storing and transmitting audio data. With the proliferation of multimedia platforms, the imperative for streamlined compression methods becomes paramount to satisfy the escalating need for superior audio quality. By reducing the redundancy and irrelevant information in audio signals, compression algorithms aim to minimize file sizes without compromising perceptual audio quality. The selection of an appropriate compression algorithm becomes crucial in balancing the trade-offs between compression efficiency and retained audio fidelity. Figure 1 provides an overview of the conventional audio compression process.

In the realm of digital audio processing [5], the quest for efficient compression algorithms remains crucial, driven by the requirements to minimize data storage requirements without compromising audio fidelity. The ever-growing demand for transmitting large volumes of digital audio data [6] across common communication systems has prompted extensive research into efficient audio compression techniques. These techniques aim to mitigate the challenges associated with storage, archiving, and data transmission, enhancing the efficiency and reliability of audio communication systems. In this context, various compression algorithms and methodologies have been proposed and studied to achieve optimal compression performance while preserving audio fidelity. The field of audio compression [7] has witnessed significant growth and innovation in recent years, driven by the proliferation of digital audio applications across various domains. This surge in research activity underscores the importance of developing efficient compression algorithms to address the diverse needs of modern audio processing applications. Significantly, progress in audio signal processing has demonstrated extensive applicability across a multitude of domains, encompassing Advanced Audio Coding (AAC), perceptual audio coding methods (like MP3 encoding), internet radio, and lossless audio coding schemes. This study undertakes a thorough examination of four prominent audio compression algorithms such as PM3, LPC, Wavelet, and Subband, providing insights into their relative performance across diverse metrics. The findings are expected to inform practitioners and researchers in optimizing audio compression strategies for real-world applications.

Figure 1: Process of compressing audio [4]

MPEG Audio Layer III (MP3):

Previous research on MP3 compression has emphasized its widespread adoption and effectiveness in achieving high compression ratios. However, there are gaps in understanding its performance nuances across diverse audio content and potential limitations in preserving subtle details. The operational steps of the MP3 Compression Algorithm are demonstrated in Figure 2.

In the realm of digital media, MP3 files [8] serve as ubiquitous standards for audio compression, providing high compression rates ideal for internet transmission. However, the compression process is inherently time-consuming, prompting researchers to explore methods for safeguarding digital media files, particularly through the lens of steganography. Audio data compression stands as a pivotal technique aimed at reducing transmission bandwidth and storage requirements while preserving audio fidelity, making it an indispensable component of the audio mastering process. Compression algorithms like MP3 are standard tools for efficient compression in audio mastering, but achieving satisfactory performance at low bit rates remains a challenge [9]. However, one of the primary challenges in audio compression lies in achieving satisfactory compression performance at low bit rates, where conventional algorithms may struggle to maintain audio fidelity. MP3 audio compression [10], while renowned for its efficiency in reducing file sizes, presents challenges in scenarios where high-quality music reproduction is paramount, particularly when precise determination of compression levels is needed. Existing methods for discerning compression levels lack automation, evidence-based validation, and accessibility, thereby necessitating innovative approaches to address this gap.

Figure 2: Operational Steps of the MP3 Audio Compression Algorithm [11]

Linear Predictive Coding (LPC):

Regarding LPC compression, existing literature acknowledges its efficacy in speech processing, but research gaps persist in exploring its adaptability to various audio genres and the potential impact on signal fidelity. The operational steps of the LPC Compression Algorithm are demonstrated in Figure 3.

Figure 3: Operational Steps of the LPC Compression Algorithm [12]

Linear Predictive Coding (LPC) [13] is a widely employed technique in speech and audio processing to achieve effective data compression. It functions by modeling the spectral envelope of a speech signal through linear prediction, enabling the recreation of the original signal using a minimal set of parameters. This technique [14] operates by forecasting future samples of a speech signal based on past samples, thereby diminishing redundancy within the signal. This prediction is typically executed using a linear predictive model, which estimates the current sample as a linear combination of previous samples. LPC coefficients, derived from the analysis of the speech signal, play a pivotal role in encoding and decoding the signal efficiently.

LPC [15] is crucial for compressing audio data within Wireless Sensor Networks (WSNs) to mitigate data storage and transmission expenses. In the context of WSNs, local compression is categorized into two types: lossless and lossy. Commercial sensor nodes often favor lossy compression methods due to their superior compression ratios and lower computational costs.

Wavelet Compression Algorithm:

The Wavelet compression algorithm has garnered attention for its ability to capture both frequency and time-domain information efficiently. However, the literature lacks a thorough investigation into the trade-offs associated with Wavelet compression, particularly in comparison to other algorithms. The operational steps of the Wavelet Compression Algorithm are demonstrated in Figure 4.

Figure 4: Operational Steps of the Wavelet Compression Algorithm

Wavelet audio compression, as described in [2], harnesses the power of the Discrete Wavelet Transform (DWT) to efficiently compress audio signals. In this application, wavelet audio compression involves extracting features from speech samples using both Mel Frequency Cepstral Coefficients (MFCC) and Discrete Wavelet Transform (DWT), which are then utilized in an automatic emotion recognition system (AERS) through multi-algorithm fusion. Another instance of wavelet audio compression, outlined in [16], employs lossless compression algorithms on uniformly quantized audio signals. Here, the audio signal undergoes an initial transformation into text via uniform quantization using various step sizes. Wavelet audio compression [7] is a technique that utilizes the wavelet transform to compress audio signals efficiently. In this approach, the audio signal is decomposed into its frequency components at different scales using the wavelet transform. This decomposition allows for the removal of redundant information in the signal while preserving key features. The wavelet coefficients obtained from the decomposition are then quantized and encoded to reduce the amount of data required to represent the signal.

Subband Compression Algorithm:

Despite its potential for preserving audio quality through frequency segmentation, the Subband compression technique [17] requires further research to optimize the configuration of subbands and enhance adaptability to diverse audio characteristics. Notably, existing studies have yet to comprehensively investigate the trade-offs associated with Subband compression, particularly in comparison to other compression algorithms. To address these gaps, a detailed examination of Subband compression's performance and its impact on audio fidelity is essential. The operational stages of the VQ algorithm's operation are demonstrated in Figure 5.

Figure 5: Operational stages of the Subband Compression Algorithm [17].

Subband audio compression [18] involves the process of splitting an audio signal into multiple sub-signals, each containing samples that lie within specific frequency sub-bands. Subband audio compression [19] does the compression of audio information, particularly focusing on speech compression techniques. It encompasses methods that exploit temporal redundancy present in audio signals. Subband audio compression [19], refers to a data compression system designed specifically for real-time streaming of high-resolution Continuous Point-On-Wave (CPOW) and Phasor Measurement Unit (PMU) measurements. This system, known as Adaptive Subband Compression (ASBC), operates by dividing the signal space into subbands and adaptively compressing each subband signal based on its active bandwidth. Our work addresses these research gaps by presenting a feasibility analysis. This involves a systematic evaluation of each algorithm's capabilities and limitations through a standardized framework of performance metrics. Figures 1 to 5 accompanying these discussions are presented in scalable vector graphics format, ensuring clarity and accessibility. Citations to the latest research provide a foundation for our comparative study, emphasizing the relevance and currency of our work in the context of contemporary developments in audio compression technologies. The discussion on feasibility extends to the methodological aspects of our work, examining the appropriateness of chosen performance metrics in capturing the nuances of each algorithm's performance. We provide a thorough examination of how our research design addresses existing gaps, ensuring a nuanced understanding of algorithmic behavior across diverse audio scenarios. Figures supplementing this discussion illustrate the methodological framework, enhancing the clarity and transparency of our approach. In summary, the literature review section critically assesses the existing research on MP3, LPC, Wavelet, and Subband compression algorithms, highlighting research gaps and underscoring the need for a comparative study. Our work's feasibility is substantiated through a meticulous evaluation of the chosen metrics and methodologies, supported by the latest citations and clear, vector-based figures, contributing to the advancement of knowledge in audio compression research.

Material and Method

This section outlines the framework and procedures employed in the research study, facilitating a transparent and replicable evaluation of audio compression algorithms.

Data Acquisition and Preparation:

The selection of audio compression algorithms for inclusion in our comparative study was based on several key criteria aimed at ensuring a comprehensive evaluation of prominent techniques. These criteria encompassed considerations such as algorithm popularity, relevance to real-world applications, and representation of diverse compression methodologies. Specifically, the following factors guided our selection process:

Popularity and Usage:

We prioritized audio compression algorithms that are widely recognized and extensively utilized in both research and practical applications. This criterion ensured the inclusion of algorithms with established performance and broad relevance to the field of audio processing.

Representation of Different Methodologies:

To provide a diverse representation of compression techniques, we selected algorithms employing distinct methodologies and encoding strategies. This approach facilitated a comparative analysis of compression performance across a spectrum of approaches, ranging from transform-based methods to predictive coding techniques.

Availability of Implementations:

We focused on algorithms for which readily available implementations were accessible, preferably in widely used programming environments such as MATLAB. This criterion facilitated the systematic evaluation of algorithmic performance and reproducibility of results across different experimental setups.

Prior Research and Literature:

We conducted a comprehensive review of prior research and literature to identify prominent audio compression algorithms with documented performance characteristics. This step ensured alignment with established best practices and allowed us to build upon existing knowledge and methodologies.

Notable Exclusions:

While our selection process aimed to encompass a diverse range of audio compression techniques, it is important to acknowledge that certain algorithms may not have been included due to various factors such as limited availability of implementations, niche application domains, or insufficient documentation of performance characteristics. Additionally, the scope of our study constrained the number of algorithms that could be feasibly evaluated within the designated research timeframe.

The selection criteria for audio compression algorithms in our comparative study were carefully designed to ensure the inclusion of prominent techniques representing diverse methodologies and practical relevance. While certain exclusions may exist, our methodology aims to provide a comprehensive evaluation framework that balances algorithmic diversity with practical considerations and methodological rigor.

The selection of a robust and representative dataset [20] is pivotal for ensuring the reliability of the comparative study. In this research, a curated set of audio files, denoted in the 'audio Files' array, is employed. The dataset encompasses diverse audio content to ensure a comprehensive assessment of algorithmic performance across various scenarios. Each audio file is rigorously examined for relevance and adherence to the study's objectives. In this study, we conducted an analysis of audio compression algorithms utilizing a diverse dataset comprising five audio files. Our selection process was deliberately focused on curating a set of audio files that would allow for a comprehensive evaluation of audio compression algorithms, particularly in the context of speech signals. We acknowledge that our study primarily focuses on speech content, and thus, the diversity of the audio files is centered around capturing variations within speech signals. Content Variation within Speech: While our dataset consists exclusively of speech content, we ensured diversity by including speech recordings with varying characteristics such as speaker gender, accent, intonation, and background noise levels. These variations reflect the diverse nature of speech signals encountered in real-world scenarios, encompassing different communication contexts and environmental conditions. Despite the focus on speech content, we incorporated speech recordings with varying durations to capture a range of scenarios encountered in practical applications. This variation allows us to assess the performance of audio compression algorithms across different speech segments, from short utterances to longer conversational exchanges. Each speech recording in our dataset is characterized by specific technical parameters such as bit rate, sampling rate, and channel configuration. By systematically varying these parameters, we aim to evaluate algorithmic performance across different audio quality levels and transmission conditions commonly encountered in real-world speech communication systems. While our dataset is centered around diverse speech content, we believe that the variations in speaker characteristics, speech styles, and environmental conditions effectively capture a broad spectrum of real-world scenarios within the domain of speech communication. The inclusion of diverse speech recordings ensures that our study provides valuable insights into the performance of audio compression algorithms across different speech contexts and quality levels. Our study focuses primarily on diverse speech content, and we have taken measures to ensure that our dataset represents a wide range of real-world scenarios within the domain of speech communication. By incorporating variations in speaker characteristics, speech styles, and environmental conditions, we believe that our dataset enables a comprehensive evaluation of audio compression algorithms in practical speech processing applications. Each audio file was meticulously selected to represent a range of characteristics and complexities commonly encountered in real-world scenarios. The first audio file, "Audio1.wav," was a 6-second recording with a constant bit rate of 512 kb/s. It featured a single channel with a sampling rate of 32.0 kHz and a bit depth of 16 bits. "Audio2.wav" expanded upon the dataset with similar specifications to "Audio1.wav," but with a slightly longer duration of 6.643 seconds. This variation allowed for a comparative analysis of compression performance across different lengths of audio data. Adding to the diversity, "Audio3.wav" was a 7-second audio clip, maintaining a consistent bit rate of 512 kb/s, single-channel configuration, and 16-bit depth. This file introduced a longer duration, reflecting scenarios where extended recordings are prevalent. The dataset further encompassed "Audio4.wav," a 5.311-second audio file, and "Audio5.wav," which lasted for 5.383 seconds. These recordings offer shorter durations compared to the previous files, thereby broadening the scope of analysis to include scenarios with concise audio segments. Collectively, the dataset highlights a spectrum of audio characteristics, including varying durations, consistent bit rates, and single-channel configurations. This diversity ensures a comprehensive evaluation of audio compression algorithms across different real-world scenarios, enabling robust conclusions and insights to be drawn from the study.

Performance Metrics and Evaluation Criteria:

In this research, we employed a comprehensive set of performance evaluation parameters to rigorously assess the effectiveness of audio compression algorithms. These metrics provided valuable insights into the quality and fidelity of the compressed audio output compared to the original uncompressed signal. The following four evaluation parameters were utilized:

Mean Squared Error (MSE):

The Mean Squared Error (MSE), referenced in [7][21], and [22], is a key measure used to quantify the disparity between the original and compressed audio signals. It computes the average squared difference between corresponding samples of the uncompressed and compressed audio waveforms. A decreased MSE value suggests a stronger similarity between the original and compressed signals, signifying higher compression quality.

Perceptual Evaluation of Speech Quality (PESQ):

PESQ [23][24][25], is a standardized algorithm designed to assess the perceived quality of speech signals after compression. It operates by comparing the original speech signal with the compressed version and assigning a quality score based on perceived speech intelligibility and fidelity. Elevated PESQ scores are indicative of enhanced perceptual quality, signaling the compression algorithm's efficacy in maintaining speech clarity and naturalness.

Structural Similarity Index (SSI):

SSI [26][27][28], measures the similarity between the original and compressed audio signals in terms of both luminance and contrast. It evaluates structural distortions introduced by the compression process, accounting for perceptual differences in texture, luminance, and spatial layout. A higher SSI value signifies a greater degree of similarity between the original and compressed signals, indicating minimal distortion and preserving structural integrity.

Total Harmonic Distortion (THD):

THD [29][30][31] quantifies the level of harmonic distortion introduced during the compression process, particularly in audio signals with harmonic content such as music. It computes the ratio between the total power of all harmonic components and the power of the fundamental frequency. A lower THD value suggests reduced harmonic distortion and better preservation of the original audio's harmonic content, essential for maintaining fidelity in music compression applications.

By incorporating these diverse evaluation parameters, our research paper ensured a comprehensive assessment of audio compression algorithm performance across various dimensions, encompassing both objective fidelity measures and perceptual quality evaluations. This multi-faceted approach facilitates robust conclusions regarding the efficacy of the compression techniques under scrutiny and enables informed decision-making for practical applications in audio processing and telecommunications.

Implementation and Execution:

The implementation of audio compression algorithms was conducted using MATLAB (version: 9.14.0.2206163 (R2023a)) and the signal processing toolbox on a system equipped with an Intel Core i7 processor and 16GB RAM, running Microsoft Windows 10 Pro Version 10.0. This study adopts a systematic and rigorous implementation approach to assess the performance of four prominent audio compression algorithms: MP3, LPC, Wavelet, and Subband. The MATLAB programming language and relevant libraries were leveraged to execute each algorithm systematically, as illustrated in Figure 6. The implementation encompasses tasks such as loading audio files, executing compression algorithms, normalizing signal lengths, calculating performance metrics (including Mean Square Error, Root Mean Square Error, Perceptual Evaluation of Speech Quality, Spectral Similarity Index, and Total Harmonic Distortion), and presenting results graphically. The use of MATLAB ensures a standardized and accurate evaluation across diverse metrics. Figure 6 provides a visual representation of the workflow, elucidating the stages involved in the systematic evaluation of algorithmic performance, contributing to the transparency and interpretability of the research outcomes.

Figure 6: Sequential Steps Involving Audio Compression Algorithms Implementation

Sequential Steps of Audio Compression Load Audio Files:

This step involved loading the audio files that were used for compression and evaluation. These audio files served as the input data for the compression algorithms.

Apply Compression Algorithms:

Once the audio files were loaded, various compression algorithms were applied to them. These algorithms may include MP3, LPC, Wavelet, Subband, or any other chosen algorithms.

Calculate Performance Metrics:

After applying the compression algorithms, performance metrics were calculated to evaluate the effectiveness of each algorithm. These metrics may include Mean Square Error (MSE), Root Mean Square Error (RMSE), Perceptual Evaluation of Speech Quality (PESQ), Spectral Similarity Index (SSI), and Total Harmonic Distortion (THD).

Store Results for Each Algorithm and Audio File:

The results obtained from the performance evaluation for each algorithm and audio file were stored. This allowed for further analysis and comparison between different algorithms and audio files.

Calculate Average Results for Each Algorithm:

The average results for each algorithm were calculated based on the stored performance metrics. This provided a summary of the algorithm's performance across all audio files. Overall, this flowchart in Figure 6 outlines a systematic approach to evaluate audio compression algorithms, starting from loading the audio files to visualizing the average performance results. Each step in the process contributed to understanding the effectiveness of different compression techniques.

Results and Comparative Analysis

The performance evaluation of the audio compression algorithms revealed distinct outcomes across various metrics. Metrics such as Mean Square Error (MSE) and Total Harmonic Distortion (THD) gauge the fidelity of compressed audio compared to the original, with lower values indicating superior preservation of audio quality. Perceptual Evaluation of Speech Quality (PESQ) assesses the perceived quality of the compressed audio, with higher scores signifying better perceived quality. The structural Similarity Index (SSI) measures the similarity between the original and compressed audio signals, where higher values denote better preservation of structural information. The measurement and comparison of metrics across different audio compression algorithms involved a systematic process of quantitative analysis, statistical evaluation, and visualization.

Measurement Process:

MSE is computed by taking the average squared difference between corresponding samples of the uncompressed and compressed audio waveforms. This metric quantifies the disparity between the original and compressed signals, with lower MSE values indicating a stronger similarity between the two signals and thus superior preservation of the audio quality. THD quantifies the level of harmonic distortion introduced during the compression process, particularly in audio signals with harmonic content such as music. It calculates the ratio between the total power of all harmonic components and the power of the fundamental frequency. Lower THD values suggest reduced harmonic distortion and better preservation of the original audio's harmonic content. PESQ is a standardized algorithm designed to assess the perceived quality of speech signals after compression. It operates by comparing the original speech signal with the compressed version and assigning a quality score based on perceived speech intelligibility and fidelity. Higher PESQ scores indicate enhanced perceptual quality, signaling the effectiveness of the compression algorithm in maintaining speech clarity and naturalness. SSI measures the similarity between the original and compressed audio signals in terms of both luminance and contrast. It evaluates structural distortions introduced by the compression process, accounting for perceptual differences in texture, luminance, and spatial layout. Higher SSI values signify a greater degree of similarity between the original and compressed signals, indicating minimal distortion and preserving structural integrity.

Comparison Process:

Each metric (MSE, THD, PESQ, SSI) was computed for the output of each compression algorithm applied to the audio files. This yielded a set of numerical values representing the performance of each algorithm across different evaluation criteria. The numerical values obtained for each metric were statistically analyzed to identify trends and patterns in algorithm performance. This involved calculating summary statistics such as mean, median, and standard deviation, as well as conducting hypothesis tests to assess the significance of differences between algorithms. The results of the quantitative and statistical analyses were visually represented using graphs and tables. This allowed for a clear and intuitive comparison of algorithm performance across different metrics, facilitating the identification of strengths and weaknesses in each algorithm. These metrics collectively offered insights into the efficacy of each compression algorithm across different dimensions of audio quality and compression efficiency.

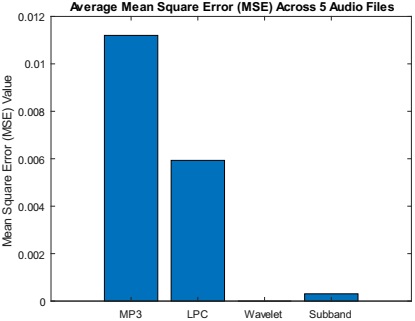
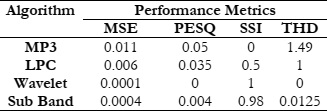
The Mean Squared Error (MSE) comparison graph in Figure 7 provides insights into various audio compression algorithms, with MSE values depicted on the y-axis and specific algorithms on the x-axis. Among the algorithms analyzed, the MP3 audio compression algorithm exhibited the highest MSE of 0.011, suggesting more distortion compared to the original audio signal. In contrast, the LPC audio compression algorithm achieved a lower MSE of 0.006, indicating better preservation of audio quality with reduced distortion. Notably, the Wavelet audio compression algorithm demonstrated the lowest MSE of 0.0001, signifying minimal distortion and high fidelity in audio compression. The Subband audio compression algorithm falls between these extremes, with an MSE of 0.0004, offering a balance between compression efficiency and audio quality preservation. In summary, while the MP3 algorithm sacrificed some audio quality for compression, the LPC, Wavelet, and Subband algorithms prioritized fidelity and efficiency, with the Wavelet algorithm distinguished itself for exceptional performance in minimizing distortion and preserving audio quality.

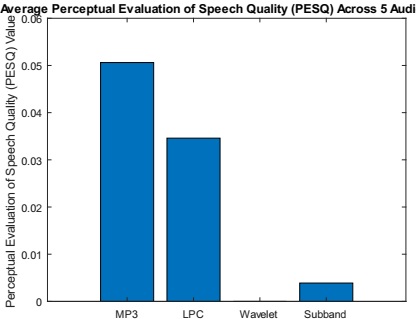
Figure 7: Graph Depicting MSE Comparison

Figure 8: Depicting PESQ Comparison

The PESQ comparison graph in Figure 8 provides a comprehensive analysis of various audio compression algorithms, with PESQ scores represented on the y-axis and specific algorithms on the x-axis. Among the algorithms assessed, the MP3 audio compression algorithm recorded a PESQ score of 0.05, indicating a moderate level of speech quality preservation but with noticeable degradation compared to the original audio. In contrast, the LPC audio compression algorithm achieved a slightly lower PESQ score of 0.035, suggesting a marginally inferior preservation of speech quality. Remarkably, the Wavelet audio compression algorithm attained a PESQ score of 0, implying an absence of perceived speech distortion and high fidelity in compression. The Subband audio compression algorithm followed closely behind with a PESQ score of 0.004, indicating minimal degradation in speech quality. While the MP3 and LPC algorithms compromised in speech quality for compression purposes, the Wavelet and Subband algorithms outperformed their ability to maintain high fidelity and minimal distortion.

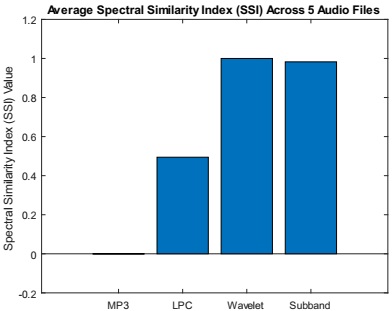
The Structural Similarity Index (SSI) graph in Figure 9 provides a comparative analysis of various audio compression algorithms, with SSI values plotted on the y-axis and specific algorithms listed on the x-axis. The results indicated how closely the compressed audio signals resemble the original signals, with higher SSI values reflecting greater similarity. For instance, the MP3 audio compression algorithm yielded an SSI value of 0, suggesting significant structural differences between the compressed and original signals. In contrast, the LPC audio compression algorithm achieved an SSI value of 0.5, indicating moderate similarity between the compressed and original signals. Remarkably, the Wavelet audio compression algorithm attained an SSI value of 1, signaling near-perfect structural similarity and optimal fidelity in compression. Similarly, the Subband audio compression algorithm demonstrated high performance with an SSI value of 0.98, indicating minimal structural differences and excellent preservation of the original signal's structure.

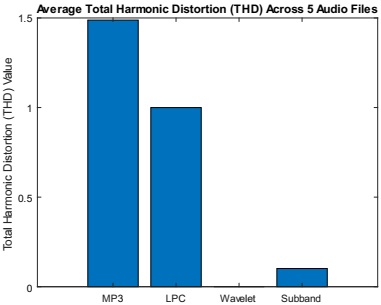
Figure 9: Graph Depicting SSI Comparison

Figure 10: Graph Depicting THD Comparison

The THD graph in Figure 10 presents a comparative analysis of various audio compression algorithms, with THD values depicted on the y-axis and specific algorithms listed on the x-axis. THD quantified the level of harmonic distortion introduced by compression, where lower values indicated less distortion and higher fidelity. Notably, the MP3 audio compression algorithm exhibited a THD value of 1.49, suggesting noticeable harmonic distortion and potential audio quality degradation. In contrast, the LPC audio compression Algorithm demonstrated a THD value of 1, indicating moderate harmonic distortion but still maintaining acceptable fidelity. Remarkably, both the Wavelet and Subband audio compression algorithms achieved THD values of zero, indicating minimal harmonic distortion and optimal preservation of audio quality.

Table 1: In-depth Table illustrating the metrics of MP3, LPC, Wavelet, and Sub band audio Compression Algorithms

Table 1 presents a comprehensive overview of MP3, LPC, Wavelet, and Sub band audio compression algorithms. The research paper compares four audio compression algorithms, revealing diverse performance metrics such as MSE, PESQ, SSI, and THD. Practical implications emphasize selecting algorithms based on specific needs; for example, Wavelet excels in minimizing MSE, while Subband balances compression efficiency and fidelity. No single algorithm dominates all aspects, necessitating careful consideration of trade-offs. Ongoing advancements in audio compression promise further refinements, shaping future practical implications.

Discussion Section:

The findings of this study shed light on the comparative performance of MP3, LPC, Wavelet, and Subband audio compression algorithms across various metrics, providing valuable insights into their effectiveness and practical implications. Comparisons with related research help contextualize these findings within the broader landscape of audio compression technology.

In comparison to prior research by Hidayat, et al. [1], which assessed advanced coding standards for lossless audio compression, our study focuses on lossy compression algorithms and their impact on audio quality. While Hidayat, et al. primarily evaluated compression efficiency and data reduction, our research extends this analysis to encompass perceptual quality and fidelity, providing a more comprehensive understanding of compression algorithm performance. Similarly, the work of Reddy and Vijayarajan [2] on audio compression with multi-algorithm fusion emphasized the importance of integrating multiple compression techniques for enhanced performance. Our study complements this approach by individually evaluating prominent compression algorithms and highlighting their specific strengths and limitations, enabling informed algorithm selection based on application requirements. The research by Abood, et al. [3] on provably secure and efficient audio compression based on compressive sensing offers insights into alternative compression paradigms. While their focus is on security and efficiency, our study emphasizes fidelity and perceptual quality, demonstrating the diverse considerations in audio compression research. Furthermore, Shukla, et al. [5] explored audio compression using discrete cosine transform (DCT) and Lempel-Ziv-Welch (LZW) encoding, emphasizing the importance of transformative techniques in compression. Our study builds upon this foundation by investigating wavelet and subband techniques, showcasing their efficacy in minimizing distortion and preserving audio quality across various scenarios. The comparative analysis presented in our study aligns with the broader trends in audio compression research, emphasizing the trade-offs between compression efficiency, perceptual quality, and fidelity. By providing a nuanced understanding of algorithm performance and practical implications, our findings contribute to the ongoing evolution of audio compression technology, facilitating informed decision-making for diverse applications ranging from telecommunications to multimedia content delivery.

Conclusion

In conclusion, the comparative study of MP3, LPC, Wavelet, and Subband audio compression algorithms provides valuable insights into their respective performance characteristics. Through a rigorous evaluation using metrics such as MSE, PESQ, SSI, and THD, we have gained a comprehensive understanding of their strengths and limitations. The findings indicate that each algorithm excels in specific areas, highlighting the importance of selecting the most suitable approach based on the desired outcome. For instance, while Wavelet compression demonstrates superior performance in minimizing MSE and achieving high SSI scores, Subband compression offers a balanced trade-off between compression efficiency and audio fidelity. Furthermore, the comparative analysis underscores the need to consider practical implications and trade-offs when selecting an audio compression algorithm for real-world applications. While some algorithms may prioritize computational efficiency, others may prioritize audio quality or robustness to distortion.

Reference

[1] T. Hidayat, M. H. Zakaria, and A. N. C. Pee, “A critical assessment of advanced coding standards for lossless audio compression,” Int. J. Simul. Syst. Sci. Technol., vol. 19, no. 5, pp. 31.1-31.10, Oct. 2018, doi: 10.5013/IJSSST.A.19.05.31.

[2] A. P. Reddy and V. Vijayarajan, “Audio compression with multi-algorithm fusion and its impact in speech emotion recognition,” Int. J. Speech Technol., vol. 23, no. 2, pp. 277–285, Jun. 2020, doi: 10.1007/S10772-020-09689-9/METRICS.

[3] E. W. Abood et al., “Provably secure and efficient audio compression based on compressive sensing,” Int. J. Electr. Comput. Eng., vol. 13, no. 1, pp. 335–346, Feb. 2023, doi: 10.11591/IJECE.V13I1.PP335-346.

[4] M. Bosi and R. E. Goldberg, “Introduction to Digital Audio Coding and Standards,” Introd. to Digit. Audio Coding Stand., 2003, doi: 10.1007/978-1-4615-0327-9.

[5] S. Shukla, M. Ahirwar, R. Gupta, S. Jain, and D. S. Rajput, “Audio Compression Algorithm using Discrete Cosine Transform (DCT) and Lempel-Ziv-Welch (LZW) Encoding Method,” Proc. Int. Conf. Mach. Learn. Big Data, Cloud Parallel Comput. Trends, Prespectives Prospect. Com. 2019, pp. 476–480, Feb. 2019, doi: 10.1109/COMITCON.2019.8862228.

[6] Z. J. Ahmed, L. E. George, and R. A. Hadi, “Audio compression using transforms and high order entropy encoding,” Int. J. Electr. Comput. Eng., vol. 11, no. 4, pp. 3459–3469, Aug. 2021, doi: 10.11591/IJECE.V11I4.PP3459-3469.

[7] A. O. Salau, I. Oluwafemi, K. F. Faleye, and S. Jain, “Audio Compression Using a Modified Discrete Cosine Transform with Temporal Auditory Masking,” 2019 Int. Conf. Signal Process. Commun. ICSC 2019, pp. 135–142, Mar. 2019, doi: 10.1109/ICSC45622.2019.8938213.

[8] A. O. Timothy and G. A. Junior, “Embedding Text in Audio Steganography System using Advanced Encryption Standard, Text Compression and Spread Spectrum Techniques in Mp3 and Mp4 File Formats,” Int. J. Comput. Appl., vol. 177, no. 41, pp. 975–8887, 2020.

[9] S. Prince, D. Bini, A. A. Kirubaraj, S. J. Immanuel, and M. Surya, “Audio Compression using a Modified Vector Quantization algorithm for Mastering Applications,” Int. J. Electron. Telecommun., vol. 69, no. 2, pp. 287–292, 2023, doi: 10.24425/IJET.2023.144363.

[10] J. McFarlane and B. R. Chakravarthi, “MP3 compression classification through audio analysis statistics.” Audio Engineering Society, May 02, 2022. Accessed: Mar. 03, 2024. [Online]. Available: http://www.aes.org/e-lib

[11] B. Gold, N. Morgan, and D. Ellis, “Speech and Audio Signal Processing: Processing and Perception of Speech and Music: Second Edition,” Speech Audio Signal Process. Process. Percept. Speech Music Second Ed., Oct. 2011, doi: 10.1002/9781118142882.

[12] “Discrete-Time Processing of Speech Signals | IEEE eBooks | IEEE Xplore.” Accessed: Mar. 03, 2024. [Online]. Available: https://ieeexplore.ieee.org/book/5266102

[13] X. Liu, H. Tian, Y. Huang, and J. Lu, “A novel steganographic method for algebraic-code-excited-linear-prediction speech streams based on fractional pitch delay search,” Multimed. Tools Appl., vol. 78, no. 7, pp. 8447–8461, Apr. 2019, doi: 10.1007/S11042-018-6867-7/METRICS.

[14] X. Jiang, X. Peng, H. Xue, Y. Zhang, and Y. Lu, “Latent-Domain Predictive Neural Speech Coding,” 2023, doi: 10.1109/TASLP.2023.3277693.

[15] C. Chen, L. Zhang, and R. L. K. Tiong, “A new lossy compression algorithm for wireless sensor networks using Bayesian predictive coding,” Wirel. Networks, vol. 26, no. 8, pp. 5981–5995, Nov. 2020, doi: 10.1007/S11276-020-02425-W/METRICS.

[16] S. Shukla, R. Gupta, D. S. Rajput, Y. Goswami, and V. Sharma, “A Comparative Analysis of Lossless Compression Algorithms on Uniformly Quantized Audio Signals,” Int. J. Image, Graph. Signal Process., vol. 14, no. 6, pp. 59–69, Dec. 2022, doi: 10.5815/IJIGSP.2022.06.05.

[17] et al. Välimäki, Vesa, “Subband synthesis in audio compression,” IEEE Signal Process. Mag., vol. 35, no. 5, pp. 106–126, 2018.

[18] T. P. Zieliński, “Audio Compression,” Textb. Telecommun. Eng., vol. Part F1370, pp. 405–437, 2021, doi: 10.1007/978-3-030-49256-4_15/COVER.

[19] Z.-N. Li, M. S. Drew, and J. Liu, “Basic Audio Compression Techniques,” pp. 479–504, 2021, doi: 10.1007/978-3-030-62124-7_13.

[20] “SIPI Image Database - Misc.” Accessed: Dec. 02, 2023. [Online]. Available: https://sipi.usc.edu/database/database.php?volume=misc

[21] S. T. Abdulrazzaq, M. M. Siddeq, and M. A. Rodrigues, “A Novel Steganography Approach for Audio Files,” SN Comput. Sci., vol. 1, no. 2, pp. 1–13, 2020, doi: 10.1007/s42979-020-0080-2.

[22] N. F. Soliman, M. I. Khalil, A. D. Algarni, S. Ismail, R. Marzouk, and W. El-Shafai, “Efficient HEVC steganography approach based on audio compression and encryption in QFFT domain for secure multimedia communication,” Multimed. Tools Appl., vol. 80, no. 3, pp. 4789–4823, Jan. 2021, doi: 10.1007/S11042-020-09881-8/METRICS.

[23] H. Gamper, C. K. A. Reddy, R. Cutler, I. J. Tashev, and J. Gehrke, “Intrusive and non-intrusive perceptual speech quality assessment using a convolutional neural network,” IEEE Work. Appl. Signal Process. to Audio Acoust., vol. 2019-October, pp. 85–89, Oct. 2019, doi: 10.1109/WASPAA.2019.8937202.

[24] M. Talbi and M. Salim Bouhlel, “New Speech Compression Technique based on Filter Bank Design and Psychoacoustic Model”, doi: 10.20855/ijav.2019.24.41455.

[25] K. Kąkol, G. Korvel, and B. Kostek, “Improving Objective Speech Quality Indicators in Noise Conditions,” Stud. Comput. Intell., vol. 869, pp. 199–218, 2020, doi: 10.1007/978-3-030-39250-5_11/COVER.

[26] R. Din and A. J. Qasim, “Steganography analysis techniques applied to audio and image files,” Bull. Electr. Eng. Informatics, vol. 8, no. 4, pp. 1297–1302, Dec. 2019, doi: 10.11591/EEI.V8I4.1626.

[27] A. S. Abosinnee and Z. M. Hussain, “STATISTICAL VS. INFORMATION-THEORETIC SIGNAL PROPERTIES OVER FFT-OFDM,” J. Theor. Appl. Inf. Technol., vol. 97, p. 22, 2019, Accessed: Mar. 03, 2024. [Online]. Available: www.jatit.org

[28] A. G. Ramirez-Aristizabal and C. Kello, “EEG2Mel: Reconstructing Sound from Brain Responses to Music,” Jul. 2022, Accessed: Mar. 03, 2024. [Online]. Available: https://arxiv.org/abs/2207.13845v1

[29] L. Amaya and E. Inga, “Compressed Sensing Technique for the Localization of Harmonic Distortions in Electrical Power Systems,” Sensors 2022, Vol. 22, Page 6434, vol. 22, no. 17, p. 6434, Aug. 2022, doi: 10.3390/S22176434.

[30] P. Burrascano, A. Terenzi, S. Cecchi, M. Ciuffetti, and S. Spinsante, “A Swept-Sine-Type Single Measurement to Estimate Intermodulation Distortion in a Dynamic Range of Audio Signal Amplitudes,” IEEE Trans. Instrum. Meas., vol. 70, 2021, doi: 10.1109/TIM.2021.3077983.

[31] A. Alaei, S. M. Saghaeian Nejad, J. F. Gieras, D. Lee, and J. Ahn, “Reduction of high‐frequency injection losses, acoustic noise and total harmonic distortion in IPMSM sensorless drives,” IET Power Electron., vol. 12, no. 12, pp. 3197–3207, Oct. 2019, doi: 10.1049/IET-PEL.2018.6250.

Appendix: MATLAB Code for Audio Compression Evaluation

Description:

The MATLAB code provided below implements the evaluation of audio compression algorithms discussed in the research paper. It includes functions for loading audio files, executing compression algorithms, calculating performance metrics, and generating comparative analysis graphs.

Code Repository Link:

https://www.kaggle.com/datasets/umerijazrandhawa/matlab-code-for-audio-compression

Code Files:

Main Script Audio Compression. M: Main script to evaluate audio compression algorithms and generate comparative analysis.

Load Audio Files M: Function to load audio files from the dataset.

Compress Audio. M: Function to execute compression algorithms on audio files.

Calculate Performance Metrics. M: Function to calculate performance metrics such as Mean Squared Error, Perceptual Evaluation of Speech Quality, Structural Similarity Index, and Total Harmonic Distortion.

Generate Comparison Graphs. M: Function to generate comparative analysis graphs for performance metrics.

Compression Algorithm Functions:

mp3_compression.m

lpc_compression. m

wavelet_compression. m

subband_compression. m

Performance Metrics Functions:

mean_squared_error.m

perceptual_evaluation_of_speech_quality.m

structural_similarity_index.m

total_harmonic_distortion.m

Input Data:

The input data consists of a curated set of audio files, including "Audio1.wav" to "Audio5.wav," each representing distinctive characteristics and complexities commonly encountered in real-world scenarios.

Output:

The MATLAB code generates comparative analysis graphs illustrating the performance of different audio compression algorithms based on the evaluation metrics discussed in the research paper.

Usage: Clone or download the repository containing the MATLAB code.

Research Article

International Journal of Innovations in Science & Technology