Estimated Zones of Saint-Venant Equations for Flood Routing with Over Bank Unsteady Flow in Open Channel
Talat Nazir, Sohail Ahmad Awan
Department of Mathematics, COMSATS University Islamabad, Abbottabad Campus, Abbottabad 22060, Pakistan.
* Correspondence: Talat Nazir talat@cuiatd.edu.pk
Citation | Nazir. T, and Awan. S. A, “Estimated Zones of Saint-Venant Equations for Flood Routing with Over Bank Unsteady Flow in Open Channel”. International Journal of Innovations in Science and Technology” Vol 3, Special Issue, pp: 96-109, 2021.
Received | Dec 9, 2021; Revised | Dec 20, 2021 Accepted | Dec 21, 2021; Published | Dec 25, 2021.
Abstract.
In this paper, we learn about the control of open channel water glide under the flood routing conditions. Generally, for flood routing in rivers, the Saint-Venant equations will be used which can be solved by finite distinction method. Saint-Venant equations will be converted into nonlinear equations and will be solved using the Preissmann scheme in the finite difference method. Using the Newton Raphson method, the set of equations will be changed into linear equations and will be solved by the space method. Our aims are to the estimated zones of Saint-Venant equations for flood routing by using the finite difference method with over bank unsteady flow in an open channel. The effectiveness of this method to optimize the choice of finite difference method is more accurate than other methods having adequate space and time steps.
Keywords: Flood routing; Saint-Venant equations; sprace method; over bank flow; hydraulic radius.
- INTRODUCTION
Over the last two decades, the study of open channel water flow has become an active research area due to its numerous advantages. It has been extensively investigated by many researchers. The hydraulic and hydrological problems involved in the computation of flood waves are based on Saint Venant (SV) equations, the pair of continuity and momentum equations. This study is important in an open channel under non-uniform or unsteady flow. It is worth mentioning that in this case SV equations cannot be solved analytically. Stoker [1] obtained the approximate solution of SV equations using the explicit finite difference method described in [2]. Ooi and Weyer [3] described the control design for an irrigation channel derived from physical data. Many researchers have obtained approximate solution of SV equations in a particular case of open channels ([4], [5], [7], [8], [9], [10], [11], [12], [13] and [14]). In these models, river waves can be categorize as gravity, diffusion, or kinematic waves, that relates to exceptional types of momentum equations.
The flood routing is fully based on the unsteady flow (long wave or surges) and the water storage equations. At the point of the channel, a flood hydrograph will find out from the well-known hydrograph at various points upstream or downstream via the known channel characters with the characteristics of side inflow or outflow between these two points. Nguyen and Kawano [15] obtained simultaneous solutions for flood routing in the open channel network by using the Preissmann method for their proposed model. Kazezylmaz-Alhan et al. [16] discussed the reliability of the finite difference method for solving proposed diffusion and kinematic wave equations that describe the overland flow. Kohne et al. [17] presented the diffusion and kinematic wave method for runoff and surplus computation. Das [18] presented the Muskingum model to find the flood path and obtained its coefficients by employing the optimization method. Sulistyono and Wiryanto [19] investigated the flood routing by dynamic wave model in the trapezoidal channels.
The main objective of this paper is to develop a quantitative method for identifying river wave types in the case of flood routing with the overbank flow. Different theoretical cases relate to the ratios between the central channel and flooded location concerning breadth and glide will be analyzed. Moreover, we define the estimated zones of SV equations for flood routing by using the Preissmann method with over bank unsteady flow in an open channel.
2. MATERIALS AND METHODS
For flood routing issues like river waves and dynamic modeling of one-dimensional, the numerical answer of SV equations will be used. In the case of the flooded region in the river, let and be the breath of the central channel and flooded region of the channel, respectively as given in Figure 1. Also let and be the cross-sectional area of the central channel and flooded region of the channel, respectively.
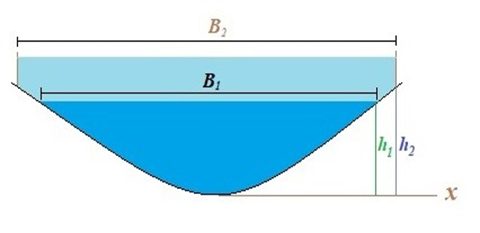
Figure 1. Open Channel having two breaths and cross-sectional areas for flow.
SV equations consist of two equations; continuity equation and momentum equation. The continuity (mass) equation is given as

where is the flow high (m), is the velocity of flow (m/s), is the acceleration due to gravity (m/s2), is energy line slope, is the slope of the riverbed, is discharge (m3/s), is the horizontal distance (m), is time (s) and the is a lateral inflow.
To derive this system, a basic assumption will be made: that there is one-dimensional flow in both regions of the channel (central region and flooded region), and there is lateral inflow or outflow.
Generally, the side channel will be rougher than the central channel. The velocity in the central region is greater than as compared to the flooded region. In this case, the Manning formula can be applied separately to both regions in determining the velocity of both channels. In this case, the manning formula might be applied one by one to every section in determining the velocity of the section. After that, the discharge in the section will be computed. The total discharge will be equal to the sum of these discharges. Since velocity in the central channel will be greater than the velocity in the flooded region so the component of discharge in the flooded area is small as compared to the discharge in the central channel; hence discharge can be approximated as follows.

Generally, in the momentum equation, the term will be calculated by the Manning formula. Since the velocity in the central region is greater than the velocity in the flooded region, thus the term of the Manning formula in the flooded region is smaller as compared to the central region of the channel. As
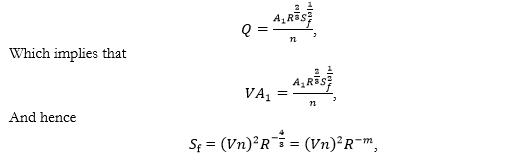

The Pressman model has a vast application in flood routing hydrograph in the open channel as given in Figure 2.
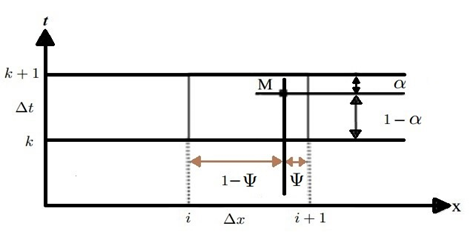
Figure 2. Preissmann method
By using above model, the time derivative is as follows

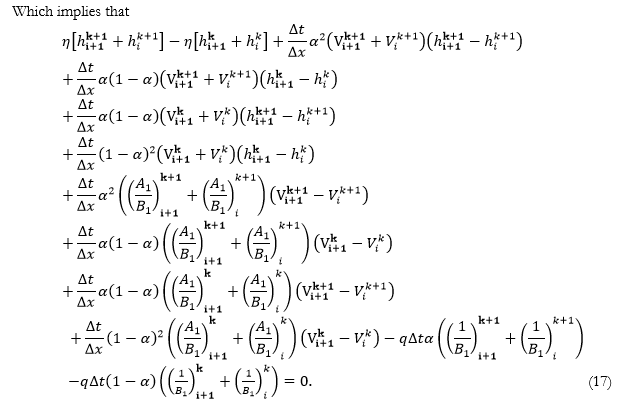



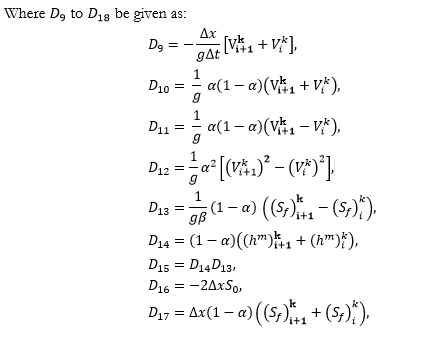

As in favor of each interval, the two vector functions and are the functions of four variables, namely. In the favor of each interval, we define two equations, and similarly, for intervalsequation will arise. For each interval,we have a node. And for each node, there will be two unknowns (flow rate and depth), thus if there are unknowns, then two equations are formed. Thus, we will obtain two more equations from up and downstream conditions [20].
Finally, a system of nonlinear equations will be generated; to change the nonlinear equations to linear, we will use the Newton-Raphson method. According to this method, the derivative of functions is given as follows
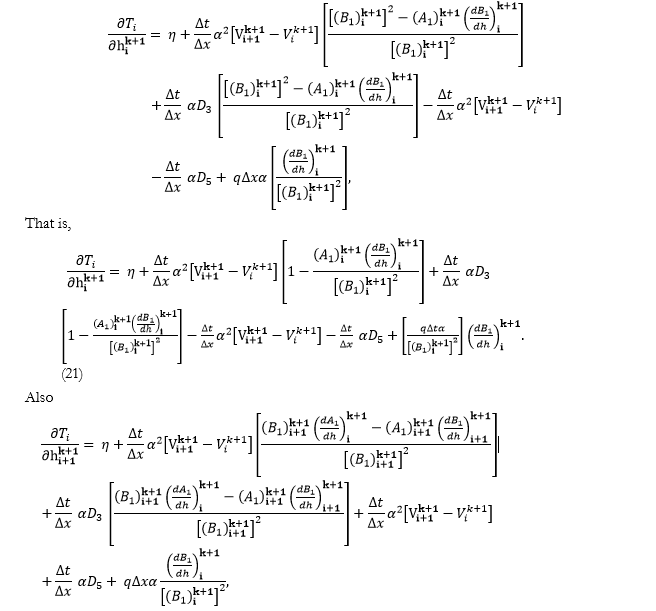
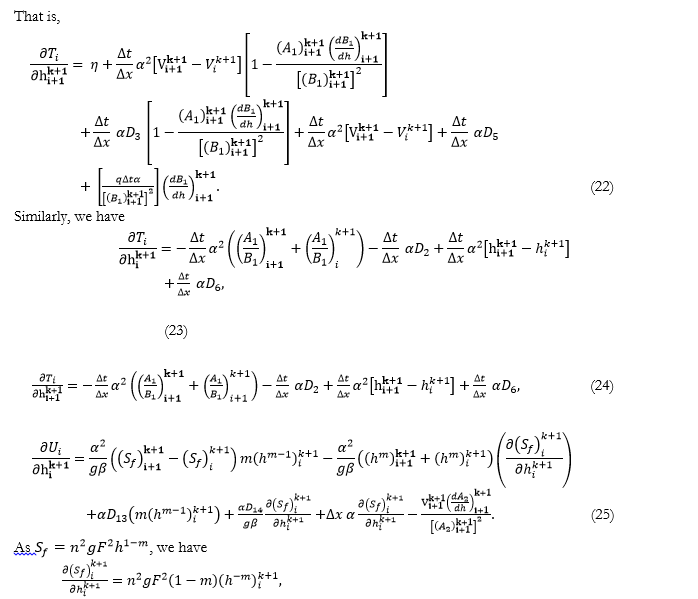


As a result, in support of interval, equations can be produced. Hence, it is ample to get the other two equations from the upstream and downstream boundary conditions, so for all nodes, two unknowns and values will be obtained. The upstream borderline (node No. 1) may additionally be the inflow hydrograph, where is the discharge of influx hydrology, and the downstream boundary circumstance (node No.) may be the glide phase, the place is the overflow height, is the overflow coefficient factor, and is the weight.
Thus, the downstream and upstream conditions are given as


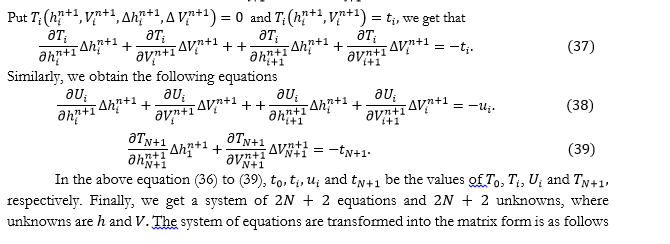

The matrix elimination programs, such as Gaussian elimination or decomposition method will be used to solve the above given system. However, Fread [9] used the Sparse characteristics of the Jacobian coefficient matrix with maximum value are considered for consecutive elements and developed an effective algorithm to solve such kind of Ribbon matrix problem. No matter which solution is used to solve the matrix, it is ultimately the case. The step is to calculate the correction value of the unknown of the next iteration. Thus, we obtain the following

Numerical Experiment. The above method requires main and boundary conditions. The main condition is a stable flow before the flow change, where the upstream condition can be flooded hydraulic pressure, and the downstream boundary condition can be a displacement relationship.
We consider a rectangular open channel with a length of , a breath of , having bed slope and a Manning roughness coefficient at the beginning of the channel is . When the flood entered with the specified water level (in flow water level) with a spillway at its end having height of , width of , and coefficient factor . Then, the water level curve and flow water level on each point will be drawn at any time by the above method. For calculations, MATLAB software has been used.
In Figures 3 and 4, the flow of water graph at and in intervals from the flood beginning point has been drawn with Preissmann scheme. According to these figures, we observed that through the increase of distance from the starting point of flood, difference between results increases.

Figure 3. Hydrographs computed at the distance from the flood start
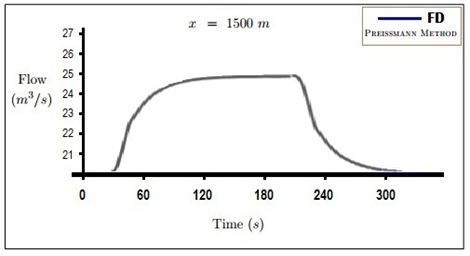
Figure 4. Hydrographs computed at the distance from the flood start.
We study the control of open channel water flow under flood routing conditions by employing the Saint Venant equations. The Saint Venant equations converted the structure of flow in the given channel into nonlinear partial differential equations which can be solve numerically by using numerical methods such as finite difference method and Newton Raphson method. By using this method, we develop iteration scheme to estimate the flow and height of water in the given channel. We also study the estimated zone of Saint-Venant equations for flood routing with over bank unsteady flow in the open channel. Some numerical experiments are also presented.
Acknowledgement. The authors are thankful to the Higher Education Commission for providing research grant to develop this work.
Author’s Contribution. All authors contributed equally to this research work of manuscript.
Project. This research work is developed under the Higher Education Commission Project no. 5398 titled "Control of open channel water flow and detecting leaks and dumps".
Conflict of interest. No conflict of interest for publishing this manuscript in IJIST.
REFRENCES
- J. Stoker, “Water waves the mathematical theory with applications” Wiley (Interscience), New York, 1957.
- O.A. Askari, M. Shayannejad, S. Eslamian, and B. Navabpour, “Comparison of solutions of saint-venat equations by characteristics and finite difference methods for unsteady flow analysis in open channel” International Journal of Hydrology Science and Technology, 2018, Vol. 8, No. 3, 229-243.
- A. Baker, “Finite-Element computational fluid dynamics” McGraw-Hill, New York, NY 1983.
- K. Ooi and E. Weyer, “Control design for an irrigation channel from physical data” Control Engineering Practice, 2008, 16 (9), 1132-1150.
- H. Chaudhry, “Open-channel flow” Springer Verlag, 2008.
- Y. Chen, K.W. Chau, and A.O. Busari, “A comparative study of population-based optimization algorithms for downstream river flow forecasting by a hybrid neural network model” Engineering Applications of Artificial Intelligence, 2015, Vol. 46, No. A, 258-268.
- H.D. Vieira, “Conditions governing the use of approximations for the saint-venant equations for shallow water flow” Journal of Hydrology, 1983, vol 60, pp: 43-58.
- C.I. Dooge and B. M. Harley, “Linear routing in uniform channel” Colorado state university, 1967.
- G. Ferrick, “Analysis of river wave types” Water Resource. Res., 1985, 21, 209-212.
- L. Fread, “Channel routing. In: Hydrological Forecasting”, M. G. Anderson and T. P. Burt (Ed.), Wiley, New York, 1985.
- W. Thiong’o, “Investigations of fluid flows in open rectangular and triangular channels” Doctoral dissertation, 2013.
- Moussa and C. Bocquillon, “Criteria for the choice of food-routing methods in natural channels” Journal of Hydrology, 1996, 186, 1-30.
- L. Wu, K.W. Chau, and Y.S. Li, “Methods to improve neural network performance in daily flows prediction” Journal of Hydrology, 2009, Vol. 372, No. 1-4, 80-93.
- Nazir, “The control of various channels water flows” IEEE Xplore, 2018 International Conference on Frontiers of Information Technology, DOI: 10.1109/FIT.2018.00066, 2018, 339-344.
- K. Nguyen and H. Kawano, “Simultaneous solution for flood routing in channel networks” Journal of Hydrology Eng. ASCE., 1995, Vol. 121, No. 10, 744-750.
- M. Kazezylmaz-Alhan, M. A. Miguel, and P. Rao, “On numerical modeling of overland flow” Applied Mathematics and Computation, 2005, Vol. 166, No. 3, 724-740.
- M. Kohne, T. Wohling, V. Pot, P. Benoit, S. Leguedois, Y. Bissonnais, and J. Simunek, “Coupled simulation of surface runoff and soil water flow using multi-objectives parameter estimation” Journal of Hydrology, 2011, Vol. 403, No. 1-2, 141-156.
- Das, “Reverse stream flow routing by using Muskingum models” Sadhana, 2009, Vol. 34, No. 3, 483-499.
- A. Sulistyono and L.H. Wiryanto, “Investigation of flood routing by a dynamic wave model in trapezoidal channels” In AIP Conference Proceedings, 2017, Vol. 1867, No. 1.
- Taormina and K.W. Chau, “Data-driven input variable selection for rainfall-runoff modeling using binary coded particles swarm optimization and extreme learning machines” Journal of Hydrology, 2015, Vol. 529, No. 3, 1617-1632.




















