Multirate Adaptive Equalization

Muhammad Yasir Siddique Anjum ¹, Muhammad Ali Raza Anjum ², Usman Riaz ³

¹ National University of Modern Languages, Pakistan.

²Army Public College of Management and Sciences, Pakistan. 

³ Centre for Advanced Studies in Engineering, Pakistan. 

* Correspondence: Muhammad Yasir Siddique Anjum <yasir.siddique@numl.edu.pk>.

Citation | Anjum. M.Y.S, Anjum. M.A.R, Riaz. U, “Multirate adaptive Equalization”, International Journal of Innovations in Science and Technology, Vol 3, Special Issue, pp: 119-125, 2022.

Received | Dec 13, 2021; Revised | Dec 18, 2021 Accepted | Dec 19, 2021; Published |Jan 1, 2022.

________________________________________________________________________

Abstract.

Finite Impulse Response (FIR) filter model emulates the Inter Symbol Interference (ISI) in a wireless communication channel. An equalizer, typically an Infinite Impulse Response (IIR) filter, behaves as an inverse filter to the FIR filter to remove the effects of the ISI. IIR filters are generally avoided due to tractability issues, and an FIR filter, with an adaptive signal processing algorithm to minimize the error due to the ISI, is deployed at the receiver. However, the filter is observed to quickly reach a steady state where further iterations do not yield a reduction in the error. This can be attributed to relatively slow variations in the steady state error which prevent further reduction of the errors. This work focuses on converting the low frequency error variations to high frequency variations by the use of multirate signal processing. As such, the steady state error can be damped as well, providing further reduction in the error and an enhanced adaptive filter performance.

Keywords: adaptive; filter; ISI; multirate; equalization. 

INTRODUCTION

It has been well established that in order to remove the effects of ISI, an equalizer has to be employed at the wireless communication receiver [1]. Two choices are available in this regard: an FIR filter and an IIR filter. FIR filters are preferred over IIR filters due to their simplicity and ease of implementation. However, FIR filters are unable to sufficiently minimize the error due to ISI, and a certain allowance has to be made for the magnitude of error in order to deploy and reap the benefits of FIR filters at the wireless communication receiver.

A well-known criterion for making such an allowance is the Minimum Mean Square Error (MMSE) criteria [2]. Many adaptive signal processing algorithms are available that try to reduce the error based on the MMSE criteria. Least Mean Square Algorithm (LMS), Normalized LMS algorithm (NLMS), and Recursive Least Squares algorithm (RLS) are popular in this regard [3,11]. These algorithms are distinguished by their implementation complexity and convergence speed, but an exclusive focus on the error analysis is not always to be found.

In iterative solvers, the error is observed to settle into a steady state after rapid initial convergence, where further iterations do not yield significant reduction in MSE [12]. This can be attributed to the ill-conditioning of the input covariance matrix, arising due to the disparity in the magnitude of its eigenvalues. Error associated with small magnitude eigenvalues dampens quickly whereas the error associated with large magnitude eigenvalues tends to linger on. Further observed is the frequency of the eigenvectors associated with large magnitude eigenvalues, which is relatively lower compared to the frequency of eigenvectors associated with small magnitude eigenvalues. These two factors, i.e., relatively large magnitude of an eigenvalue and the low frequency of its associated eigenvector, causes the MSE to settle into the steady state early, where in further reduction in MSE with increased number of iterations is not possible.

In this work, we proposed that the magnitude of larger eigenvalues can be reduced and the low frequencies of their associated eigenvectors can be converted to high frequencies by down sampling the error vector, wgicg will cause the error associated with large magnitude eigenvalues to dampen quickly as well. In this way, MSE can be reduced further and the filter convergence can be enhanced. This is the premise behind the presented work.

EQUALIZATION IN WIRELESS COMMUNICATION SYSTEMS

The equalization problem. Basic model of the equalization problem in a wireless communication system is depicted in Figure 1 [2].

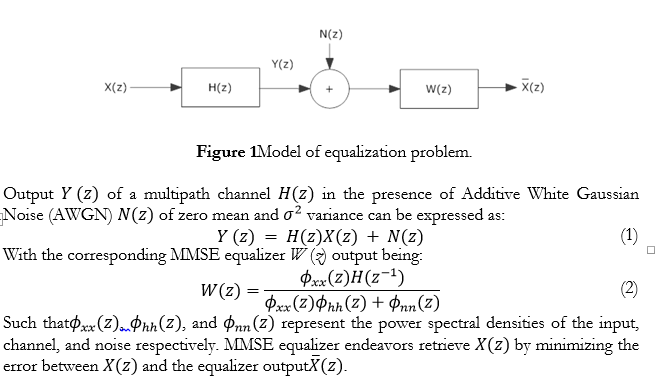
Adaptive solution to equalization problem. Adaptive solution to the equalization problem is depicted in Figure 2.

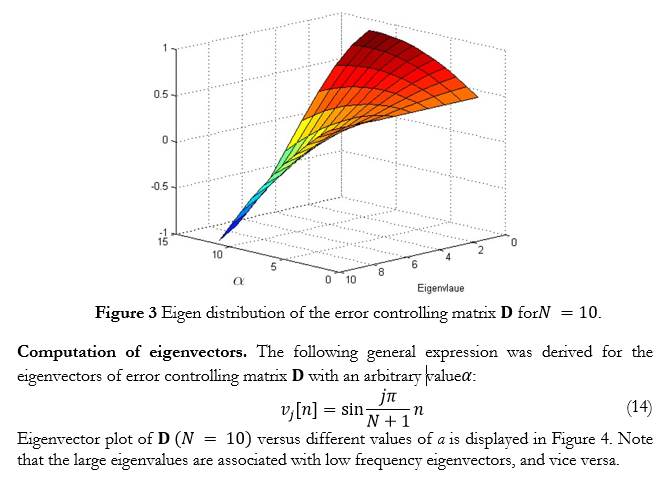
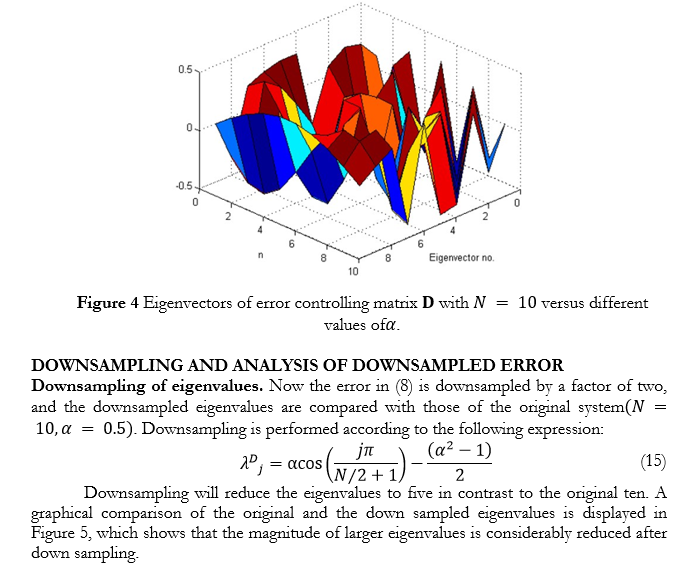
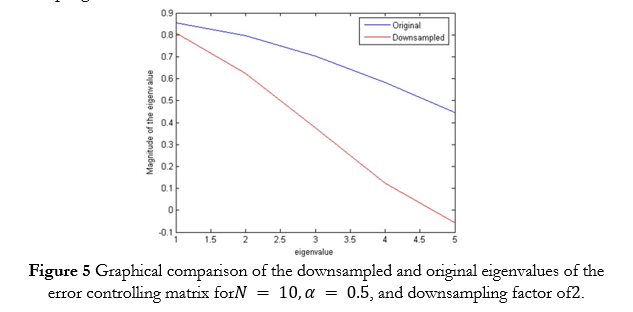
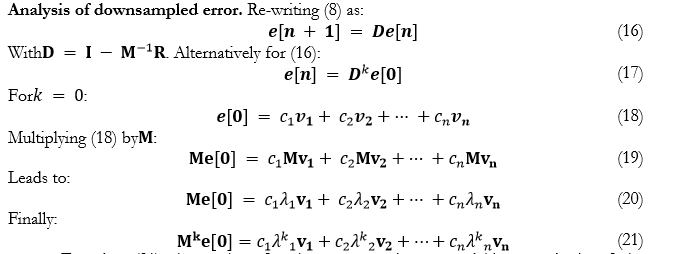
Equation (21) shows that, for the error to dampen quickly, magnitude of the eigenvalues should be as small as possible; ideally, they must be zero. However, due to the poor conditioning of the input covariance matrix, a disparity can be found in the magnitude of eigenvalues. Large magnitude eigenvalues cause the error to enter into a steady state and prevent further reduction of MSE. The steady state error can be reduced by downsampling the error vector, which makes the associated eigenvalues to dampen quickly as well when their higher powers are taken in to account according to (21). A plot of the MSE achieved from the original and the downsampled error sequence is displayed in Figure 6. The plot confirms that the downsampled error reduces much faster than the original one.

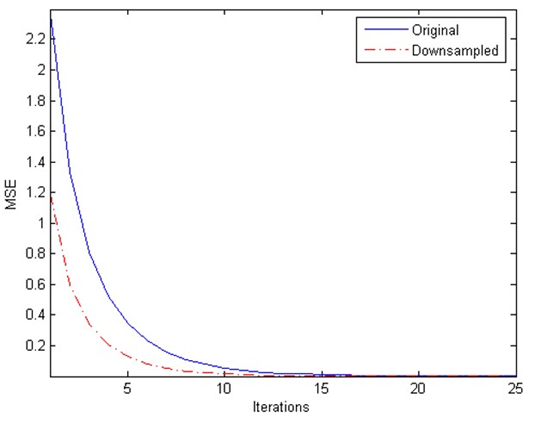
Figure 6 Comparison of the MSE achieved from the original and the downsampled error sequence.

CONCLUSION

An improvement in the error performance of adaptive wireless channel equalizer was found by downsampling the error vector by a factor of two. The improvement was demonstrated analytically and numerically. Further possibilities for improvement in error performance of adaptive equalizer can be explored by increasing the downsampling factor beyond two.

Acknowledgement. No funding to declare.

Author’s Contribution. Muhammad Yasir Siddique Anjum wrote the first draft of the manuscript, and conducted the data analysis. Muhammad Ali Raza Anjum provided technical expertise of multirate signal processing, and helped edit the manuscript. Usman Riaz supervised the study, provided factual review, and helped edit the manuscript.

Conflict of interest. There exists no conflict of interest for publishing this manuscript.

Project details. The research was not conducted as a part or result of a project.

REFRENCES

1.      T. S. Rappaport et al., “Wireless communications: principles and practice”. prentice hall PTR New Jersey, 1996, vol. 2.

2.      B. Farhang-Boroujeny, “Adaptive filters: theory and applications” John Wiley & Sons, 2013.

3.      M. Umer, “Adaptive lms based channel equalization,” International Journal of Technology and Research, vol. 2, no. 4, p. 111, 2014.

4.      R. Martinek and J. Zˇ´ıdek, “The real implementation of nlms channel equalizer into the system of software defined radio,” 2012.

5.      S. K. Sahoo and M. N. Mohanty, “Effect of ber performance in rls adaptive equalizer,” International Journal of Advanced Computer Research (IJACR), vol. 2, no. 4, 2012.

6.      R. A. Fayadh, F. Malek, H. A. Fadhil, N. A. Al-Shareefi, H. Saad et al., “Mmse equalized rake-receiver using adaptive filter with a family of partial update algorithms in wireless communication systems,” International Journal of Engineering and Technology (IJET), vol. 5, no. 6, pp. 5169–5177, 2014.

7.      R. Candido, M. Eisencraft, and M. T. Silva, “Channel equalization for synchronization of chaotic maps,” Digital Signal Processing, vol. 33, pp. 42–49, 2014.

8.      R. N. Devi, T. Saikumar, and K. K. Rao, “Nlms algorithm based cma channel equalization through an adaptive mmse equalizer,” in Proceedings of the International Conference on Information Systems Design and Intelligent Applications 2012 (INDIA 2012) held in Visakhapatnam, India, January 2012. Springer, 2012, pp. 679–688.

9.      Research progress of low-altitude wireless channel modeling and equalization techniques

10.  B. Alshehry, A. Odeh, and E. Abdelfattah, “Adaptive equalization: Lms, rls and cma,” 2014.

11.  J. Ai, G. Yue, X. Cheng, and S. Li, “Low complexity rls channel estimation for sc-fde in 60 ghz communications,” in 2012 IEEE 14th International Conference on Communication Technology. IEEE, 2012, pp. 186–191.

12.  S. Gilbert, “Computational science and engineering,” Massachusetts Institute of Technology, Wellesley-Cambridge Press, Massachusetts, USA, 2007.