Numerical Analysis of Impact of Relative Humidity on Crossflow Heat Exchangers with Staggered Configuration at Maximum Operating Temperature
Arshan Ahmed1, Atta ul Mannan Hashmi1, Fahad Rafi Butt2, Shahbaz Ghani1 and Imran Akhtar1
1 Department of Mechanical Engineering, NUST College of Electrical and Mechanical Engineering, National University of Sciences and Technology, Islamabad, Pakistan.
2 Research Associate, Digital Pakistan Lab, NUST College of Electrical and Mechanical Engineering, National University of Sciences and Technology, Islamabad, Pakistan.
* Correspondence: Arshan Ahmed; arshan721@yahoo.com.
Citation | Ahmad. A, Hashmi. A. M, Butt. F. R, Ghani. S and Akhtar. I. “Numerical Analysis of Impact of Relative Humidity on Crossflow Heat Exchangers With Staggered Configuration at Maximum Operating Temperature”, International Journal of Innovations In Science and Technology, Special Issue, pp: 84-95, 2021.
Received | Dec 14, 2021; Revised | Jan 08, 2022 Accepted | Jan 12, 2022; Published | Jan 14, 2022
Heat exchangers are employed in numerous applications of industry, automotive and air conditioning systems. The efficacy of heat exchangers depends upon various factors e.g., Reynolds number (Re) of the fluids, geometry of heat exchanging surfaces, and the Prandtl number of the cooling air. In this paper, the working of a crossflow heat exchanger with elliptical tubes is simulated numerically for 5000 < Re < 20000 at its maximum operating temperature of 323K. The tubes were arranged in a staggered way. The radical investigations were done at one-of-a-kind relative humidity ranges within the cooling air ranging from 0% to 80%. The relative humidity was modeled in the shape of mass fractions of water vapors in the air. The thermos-physical properties of dry and moist air were employed for the analysis. The impact of this changing of relative humidity on forced convection heat transfer of heat exchangers is examined in the form of percentage change in Nusselt number. With the increase in moisture content in the air, the Nusselt number was observed increased up to 4.5%. The paper provides a tool to analyze the Nusselt number of the elliptical-shaped heat exchanger while operating in moist atmospheric conditions.
Keywords: Heat transfer; relative humidity; Nusselt number; Prandtl number and Reynolds number.
INTRODUCTION
Heat exchangers are used in numerous industrial applications to transfer heat from one fluid to another. The efficacy of the amount of heat transfer depends upon various factors including Reynolds number (Re), area of heat transfer surfaces, and Prandtl number (Pr) of air. The case in which heat transfer from the surface requires external means to move the fluid over it, is termed Forced Convection Heat Transfer (FCHT). For higher velocities, natural convection heat transfer through buoyant forces is considered negligible as compared to FCHT. Nusselt number (Nu) provides the means to access the temperature gradient in the non-dimensional form and in this paper, the Nusselt number presented depends only on forced convection. Heat exchanger used for the analysis is of crossflow type with a staggered arrangement of tubes having an elliptical shape.
Different types of performance analysis with changing parameters have already been done on heat exchangers other than humid air, especially in forced convection mode. Suyi and Shizhou [1] devised correlations for Nu depending upon Reynolds and Prandtl numbers of air up to the longitudinal and transverse pitch (SL/ST) ratio of 4. Iskra and Simonson [2] developed a relationship for convective mass transfer as a function of Reynolds number and relative humidity in a rectangular duct. Reynoso-jardón et al. [3] numerically conducted an analysis of crossflow heat exchangers for increased heat transfer by varying the transverse and longitudinal pitches. Sayed Ahmed et al. [4] concluded that for a staggered wing-shaped bundle of tubes Nusselt number increases with Reynolds number and it reaches its maximum value with the angle of attack of 45 degrees. Kanthimathi et al. [5] numerically deduced that increasing the array of tubes has an increasing effect on heat transfer. Gharbi et al. [6] came up with an expression for Nusselt number based on Reynolds number for the range 5000 < Re < 25000 under specified conditions.
Still et al. [7] carried out experiments to calculate the effect of relative humidity on convective heat transfer of small cylinders in controlled conditions. They concluded that the relationship of heat transfer rates in dry and humid air is only a function of the molar fraction of water vapors in the air and does not depend on the Reynolds number and temperature of the air. Uguru-okorie and Ikpotokin [8] compared staggered and aligned tubes configurations for heat transfer rates experimentally and found an increase of 4.28% in a staggered configuration. Zhang et al. [9] numerically forecasted the change occurring in Nusselt number of natural convection heat transfer at different temperatures with relative humidity. Zukauskas & Ulinskas [10] presented the correlations for heat transfer and pressure drop for aligned and staggered crossflow heat exchangers in the range of 1000 <Remax< 2 × 106 with 0.7 <Pr< 500 and ST/SL< 0.7.
From the literature assessment, it could be deduced that elliptical-fashioned tubes provide better warmth transfer costs in comparison to other shapes at exceptional Reynolds numbers. Apart from other design and overall performance analyses, research for the impact of various air properties in terms of relative humidity on the elliptical-formed tubes heat exchanger is essential to gauge its performance in a damp ecosystem.
This novel work gauges the efficiency in the form of exchange in Nusselt quantity of warmth exchangers due to trade in relative humidity of the cooling air on the most working temperature which the heat exchanger comes throughout at its operation. The trade that is predicted to come back relies upon the thermos-physical houses of air. The alternate has been investigated at the variety of maximum Reynolds numbers which the warmth exchanger comes to throughout some point of its operation i.e. 5000 < Re < 20000.
PROBLEM SETUP
Model Characteristics. The heat exchanger available in the facility has been used for the analysis. It is a crossflow heat exchanger with elliptical-shaped tubes with a staggered arrangement. The major and minor axis ratio of the tubes of the heat exchanger is 5.76. Heat exchanger has a total of 1140 × water tubes divided equally into two flow-pass configurations. The tubes are divided into 7 × staggered rows with transverse and longitudinal pitches mentioned in Figure 1. The air flows over the bank parallel to the longitudinal axis of the tube. The inlet air is uniform with constant dynamic viscosity and thermal conductivity as per the relative humidity [11].
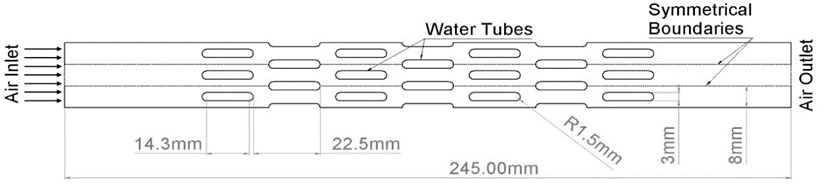
Figure 1. Geometry details and boundary conditions.
Boundary Conditions. The air outlet was ready as a pressure outlet. Symmetric boundary situations were carried out at the lateral obstacles of the area. The investigations were completed on the maximum air temperature of 323K which the warmth exchanger faces during its operation inside the facility. 323K was also set as the working temperature for the simulation. Thermo-bodily houses of air were also considered at an identical temperature [11]. The range of Reynolds number, already described, for the analysis encompasses the ambit of air velocities which heat exchanger faces in its operation. The relative humidity was introduced in the air in the form of mass fractions of water vapors using the species transport model in Ansys Fluent®. The variation of mass fraction of water vapors concerning relative humidity [12] at 323K is shown in Figure 2.
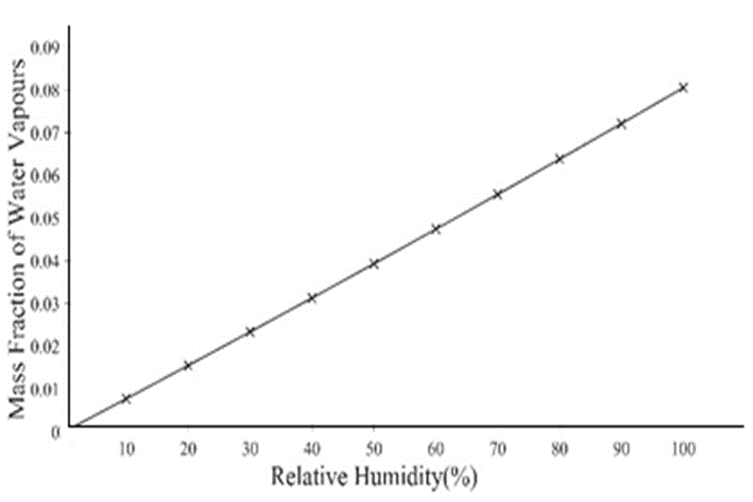
Figure 2. Mass fraction of water vapors with respect to relative humidity in air at 323K.

Figure 3. Thermal conductivity of air at 323K

Figure 4. Dynamic viscosity of air at 323K.
To minimize the effect of turbulence on heat transfer, turbulence intensity was set to 5% for all the cases of Reynolds numbers. At the measured water flow rate of 1.95 x 10-5m3/sec per tube and assuming the waterside temperature difference as 10K, the tube walls were kept at a constant heat flux of 11500 W/m2. Tubes walls were also applied with no-slip boundary conditions. Along with symmetric boundary conditions, lateral boundaries have zero diffusive flux. In the analysis, the air was treated as an ideal gas and its specific heat was calculated by applying the mixing law [13]. Thermal conductivity and dynamic viscosity of humid air with different relative humidity levels [11] at 323K were shown in Figure 3 and figure 4 respectively. The fluid properties were considered constant at the specified humidity levels. Gravity was assumed to be acting in the direction of airflow while the buoyancy and radiation effects were neglected being minimal.
Ansys Fluent® was used for solving the governing equations of the grid with quadrilateral volumes for this model to the minimal scaled residual level of 10-6. The pressure speed coupling approach with the okay-ε turbulence model was used to solve the computational grid because for fixing the elliptical bank of tubes, the prediction of the RNG model was far better than popular-ε turbulence models [14], so the former was used inside the analysis. The coupled scheme was used to clear up the discretized shape of equations. Second-order upwind method was followed for momentum and turbulent kinetic strength equations.
The geometry was modeled using the two-dimensional based grid with y+ ≈ 1. To make sure that the solution was impartial of mesh size and density, a mesh independence test [15] was achieved for the calculation of the average Nusselt variety. In the mesh independence study, the solution becomes independent of the grid when the number of cells reaches 386869. The zoomed grid was depicted in Figure 5.

Figure 5. Blow-up of a single tube in computational domain grid.
The dimensionless temperature gradient on the surface due to convective warmness within the form of the Nusselt number is dependent on the Reynolds and Prandtl numbers [16]. A variety of literature on the effect of Reynolds numbers on the convective heat transfer of elliptical-shaped tubes is already available, so in this paper, the concentration is kept on the analysis of the influence of relative humidity on the Nusselt number of elliptical-shaped tubes heat exchanger.
Before performing the analysis, the CFD model is validated with the one presented by Gharbi et al. [6] within the range 5000 < Re < 20000. During validation, the mass fraction of water vapors in the inlet is set to zero so that the heat transfer process involves dry air only. The comparison of the results is presented in Figure 6. Both the models show the same trend of rising in Nusselt number with the increasing Reynolds number with the maximum results' deviation of 7.5%. Contours of static temperature at 323K for the range of Reynolds number as displayed in Figure 8. depict the change in the thermal boundary layer with the change in Reynolds number, attributing to greater Nusselt numbers at higher velocities.
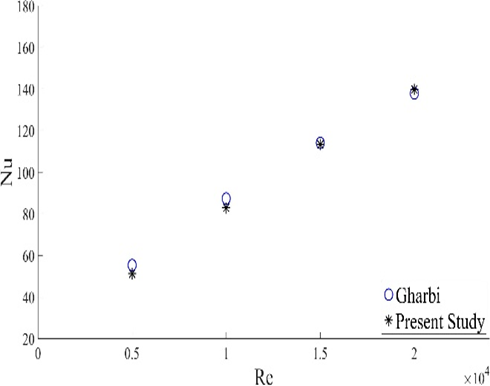
Figure 6. Model validation for Nu versus Re.
METHODOLOGY FOR HEAT TRANSFER CALCULATIONS
The amount of heat required to be dissipated from the water was calculated using the equation:

Results and Discussion
Influence of Relative Humidity (Mass Fraction of Water Vapours) on Nusselt Number.
In the analysis, as already stated, the relative humidity is simulated in the form of mass fractions of water vapors in the air. The greater the relative humidity, the greater will be the mass fraction. Mass fraction also depends upon the temperature of the air. Water content at higher temperatures will be more in the air as compared to the lower temperatures at the same humidity levels. However, for the case in this paper, the temperature of the inlet air is kept only at 323K. With the change in relative humidity, the thermophysical properties of the air were observed changed and thus the Prandtl number.
Since the Nusselt number is depending on the Prandtl range, so it also adjustments with the trade-in relative humidity. In this paper, this alteration has been calculated numerically the usage of the CFD code within the shape of percentage exchange in Nusselt quantity for relative humidity from 0% to 80%.
The share of relative humidity is numerous from 0% to eighty% with an increment of 20% at the range of the Reynolds range already mentioned. The results show that the Nusselt range are adjusted with the trade-in relative humidity. This transformation is attributed to the trade-in Prandtl wide variety of the air with the variant within the relative humidity. At 323K, the functionality of air to preserve water content material increases significantly with the boom in the percentage of relative humidity. For that reason, growing the warmth switch coefficient of the air has increased the Nusselt variety. The same can also be defined from the fact that the molecular weight of the air with 0% humidity content material is greater than that of water vapors and with the aid of increasing the humidity ratio in the air, its molecular weight decreases and it will increase the Nusselt quantity.
The change in molecular weight or density becomes more pronounced when the water content in the air increases. Thus, the change in Nusselt number becomes more pronounced at higher relative humidity levels. The percentage change in the Nusselt number concerning relative humidity at 323K is presented graphically in Figure 7.
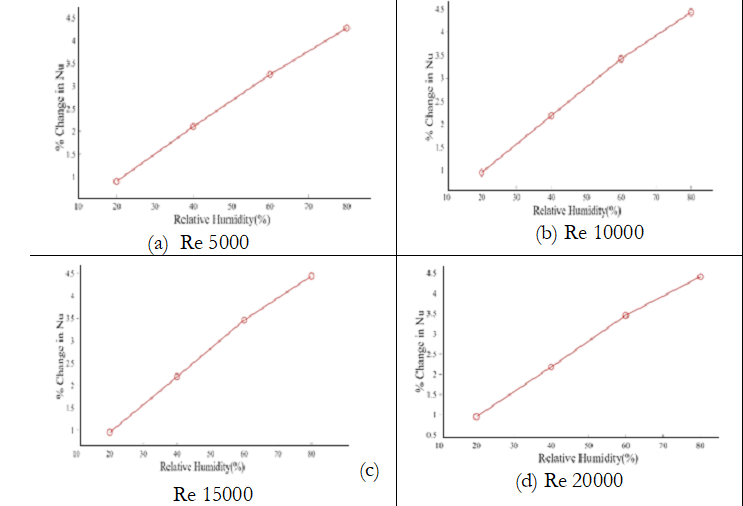
Figure 7. Change in Nu with relative humidity at 323K for different Re.
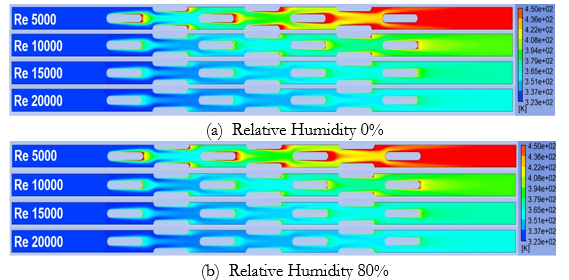
Figure 8. Temperature contours for range of Re at minimum and maximum relative humidity levels at inlet temperature 323K.
The heat transfer coefficient was observed increased with the increase in Reynolds number and relative humidity. For the range of Reynolds number selected for the study, the change produced in the Nusselt number due to the change in humidity content of air that was observed independent of Reynolds number.
Conclusion.
Relative humidity affects the thermos-physical properties in the air, which influence the airside Nusselt number of heat exchanger. This effect has been calculated and analyzed using the CFD code at 323K on a crossflow heat exchanger with elliptical-shaped tubes arranged in a staggered fashion. Prandtl number changes with an increase in relative humidity of the air. From the analysis, it can be concluded that the change in Nusselt number due to the change in relative humidity in air does not depend on the Reynolds number. The Nusselt number changes up to 4.5% by increasing the relative humidity from 0% to 80% at 323K. The share exchange in Nusselt, wide variety with the increase in relative humidity will grow if the operating temperature is elevated because the ability of air to maintain water vapors increases with the temperature upward thrust. In similar manner, the proportion will lower upon lowering the running temperature. In the same way, the percentage will decrease upon lowering the operating temperature.
Acknowledgement. This manuscript has not been published or submitted to other journals previously. This research is supported by NUST College of Electrical & Mechanical Engineering, National University of Sciences and Technology, Pakistan.
Author’s Contribution. Arshan Ahmed and Atta ul Mannan Hashmi developed the theory and performed the numerical computations. Fahad Rafi Butt verified the analytical results. Shahbaz Ghani and Imran Akhtar conceived the idea to investigate the effect of relative humidity on Nusselt number and supervised the findings of this work. All authors discussed the results in detail and contributed to the final manuscript.
Conflict of interest. The authors declare no conflict of interest for publishing this manuscript in IJIST.
REFRENCES
[1] H. Suyi and P. Shizhou, “Convection and heat transfer of elliptical tubes” “Heat Mass Transfer” 1995, vol. 30, no. 6, pp. 411–415.
[2] C. R. Iskra and C. J. Simonson, “Effect of humidity on the convective mass transfer coefficient in a rectangular duct” “Saudi Medical Journal” 2012, vol. 33, pp. 3–8.
[3] E. Reynoso-jardón, G. Urquiza, O. Tenango-pirin, and Y. Mariaca-beltrán, “Numerical study of a cross flow heat exchanger varying the transverse and longitudinal space to increase heat transfer” “International Journal of Combinatorial Optimization Problems and Informatics” 2020, vol. 11, pp. 106–114.
[4] S. A. E. Sayed Ahmed, E. Z. Ibrahiem, O. M. Mesalhy, and M. A. Abdelatief, “Heat transfer characteristics of staggered wing-shaped tubes bundle at different angles of attack,” “Heat Mass Transfer” 2014, vol. 50, no. 8, pp. 1091–1102.
[5] T. Kanthimathi, P. Bhramara, and G. N. S. Ram, “Numerical analysis on the effect of heat Transfer rate by varying the tube arrays in a cross-flow heat exchanger” “International Journal of Scientific & Engineering Research” 2016, vol. 7, no. 6, pp. 13–16.
[6] N. El Gharbi, A. Kheiri, M. El Ganaoui, and R. Blanchard, “Numerical optimization of heat exchangers with circular and non-circular shapes” “Case Studies in Thermal Engineering” 2015, vol. 6, pp. 194–203.
[7] M. Still, H. Venzke, F. Durst, and A. Melling, “Influence of humidity on the convective heat transfer from small cylinders” “Experiments in Fluids” 1998, vol. 24, no. 2, pp. 141–150.
[8] D. Uguru-okorie and I. Ikpotokin, “Experimental comparison of staggered and in-line tube- bank thermal performance” “International Journal of Mechanical Engineering and Technology” 2018, vol. 9, pp. 1061–1070.
[9] J. Zhang, A. Gupta, and J. Baker, “Effect of relative humidity on the prediction of natural convection heat transfer coefficients” “Heat Transfer Engineering” 2007, vol. 28, no. 4, pp. 335–342.
[10] B. Prasad, A. Tawfek, and V. Rao, “Heat transfer from aerofoils in cross-flow” “International Communications in Heat and Mass Transfer” 1992, vol. 19, no. 6, pp. 879–890.
[11] P. T. Tsilingiris, “Thermo-physical and transport properties of humid air at temperature range between 0 and 100°C” “Energy Conservation and Management” 2008, vol. 49, no. 5, pp. 1098–1110.
[12] Water moisture content of humid air calculator, http://www.quadco.engineering. com/en/know-how/cfd-calculate-water-fraction-humid-air. html.
[13] ANSYS Inc, “ANSYS Fluent® User’s Guide” 2013, Release 15.
[14] L. M. Smith and W. C. Reynolds, “On the Yakhot-Orszag renormalization group method for deriving turbulence statistics and models,” “Physics of Fluids A: Fluid Dynamics” 1992, vol. 4, no. 2, pp. 364–390.
[15] Importance of mesh independence study & why you should care, https://www. maxshear.com/training/importance-of-mesh-independence-study-amp-why-you-should-do-it.
[16] F. P. Incropera, D. P. Dewitt, T. L. Bergman, and A. S. Lavine, “Fundamentals of heat and mass transfer” “John Willey & Sons” 2006, ed. 6th, p. 370.
[17] A. Zukauskas, “Heat Transfer from tubes in crossflow” “Advances in Heat Transfer” 1972, vol. 8, pp. 93–160.




















