Machine Learning-Based Estimation of End Effector Position in Three-Dimension Robotic Workspace

Hamna Baig; Ejaz Ahmed; Ihtesham Jadoon

Authors

Hamna Baig Department of Electrical and Computer Engineering COMSATS University Islamabad Attock Campus Attock, Pakistan.
Ejaz Ahmed Department of Electrical Engineering Aero Space and Aviation, Air University Islamabad Kamra Campus Attock Pakistan)
Ihtesham Jadoon Department of Electrical and Computer Engineering COMSATS University Islamabad Attock Campus Attock, Pakistan.

Keywords:

Robotics, Artificial Neural Network (ANN), Denavit-Hartenberg (D-H), Prediction and Machine Learning.

Abstract

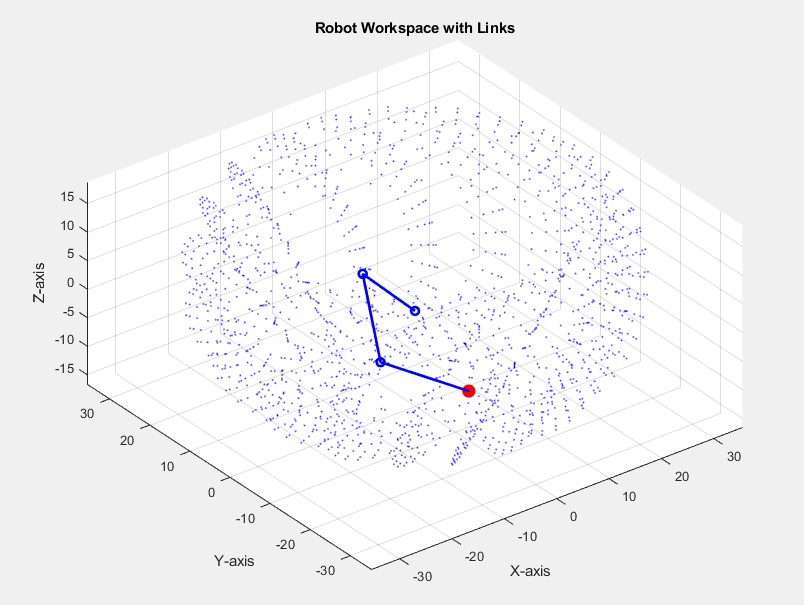
Introduction/Importance of Study: The Workspace is the area around the robot where a robot can freely move with possible input variations of different joint angles.

Novelty statement: Conventionally iterative simulation methods are used to find robotic workspace. Which are computationally slow and difficult to model. Our approach utilizes machine-learning algorithms to predict the workspace and position of an end effector.

Material and Method: Multiple Linear Regression (MLR), Decision-Tree Regression, and Artificial Neural Network (ANN) algorithms trained for prediction. The dataset, which is collected and used as train and test data, is further for the validation step.

Result and Discussion: By simulating the robot with the Denavit-Hartenberg (D-H) approach in MATLAB. The results findings show the accuracy of Machine learning algorithms specifically Artificial Neural Networks (ANN) perform better than conventional mathematical methods

Concluding Remarks: Artificial Neural Network (ANN) outperformed other machine learning methods.

References

“Forward and Inverse Kinematics Solution of A 3-DOF Articulated Robotic Manipulator Using Artificial Neural Network | Sharkawy | International Journal of Robotics and Control Systems.” Accessed: May 05, 2024. [Online]. Available: https://pubs2.ascee.org/index.php/IJRCS/article/view/1017

O. Carbajal-Espinosa, L. Campos-Macías, and M. Díaz-Rodriguez, “FIKA: A Conformal Geometric Algebra Approach to a Fast Inverse Kinematics Algorithm for an Anthropomorphic Robotic Arm,” Machines, vol. 12, no. 1, p. 78, Jan. 2024, doi: 10.3390/MACHINES12010078/S1.

E. Bayro-Corrochano, “A Survey on Quaternion Algebra and Geometric Algebra Applications in Engineering and Computer Science 1995-2020,” IEEE Access, vol. 9, pp. 104326–104355, 2021, doi: 10.1109/ACCESS.2021.3097756.

J. Denavit and R. S. Hartenberg, “A Kinematic Notation for Lower-Pair Mechanisms Based on Matrices,” J. Appl. Mech., vol. 22, no. 2, pp. 215–221, Jun. 1955, doi: 10.1115/1.4011045.

I. Virgala, M. Kelemen, M. Varga, and P. Kuryło, “Analyzing, Modeling and Simulation of Humanoid Robot Hand Motion,” Procedia Eng., vol. 96, pp. 489–499, Jan. 2014, doi: 10.1016/J.PROENG.2014.12.121.

R. Gao, “Inverse kinematics solution of Robotics based on neural network algorithms,” J. Ambient Intell. Humaniz. Comput., vol. 11, no. 12, pp. 6199–6209, Dec. 2020, doi: 10.1007/S12652-020-01815-4/METRICS.

M. Soori, B. Arezoo, and R. Dastres, “Artificial intelligence, machine learning and deep learning in advanced robotics, a review,” Cogn. Robot., vol. 3, pp. 54–70, Jan. 2023, doi: 10.1016/J.COGR.2023.04.001.

N. Kovincic, H. Gattringer, A. Müller, and M. Brandstötter, “A Boosted Decision Tree Approach for a Safe Human-Robot Collaboration in Quasi-static Impact Situations,” Mech. Mach. Sci., vol. 84, pp. 235–244, 2020, doi: 10.1007/978-3-030-48989-2_26.