Numerical Simulation of Flow Past a Square Object Detached with Controlling Object at Various Reynolds Number

Raheela Manzoor; Bushra Habib; Shazia kalsoom; Neelofer Jamil; Misbah Haque

Authors

Raheela Manzoor Department of Mathematics, Sardar Bahadur Khan Women's University, Quetta, Baluchistan, Pakistan
Bushra Habib Department of Mathematics, Sardar Bahadur Khan Women's University, Quetta, Baluchistan, Pakistan
Shazia kalsoom Department of Mathematics, Sardar Bahadur Khan Women's University, Quetta, Baluchistan, Pakistan
Neelofer Jamil Department of Mathematics, Sardar Bahadur Khan Women's University, Quetta, Baluchistan, Pakistan
Misbah Haque Department of Management Science, Mir Chakkar Khan University, Sibi, Pakistan

Keywords:

Vortex Shedding, Reynolds numbers, Flow control, Force Statistics, Drag and lift Coefficients.

Abstract

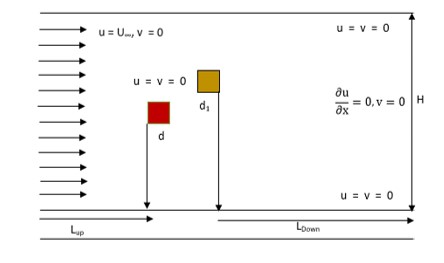
A two-dimensional (2-D) numerical study has been conducted for flow past of two different configurations of square objects by using the numerical technique Lattice Boltzmann Method (LBM). In these configurations, one object plays the role of the main object, while the second object acts as a controlling object positioned in two different ways, such as firstly placed at the top right corner of the main object (first configuration) and in the second configuration the control object is put at the bottom right corner of the main object at L = 20d (where d is the size of the object). The primary goal of this study was to investigate the impact of the control object on the main object to reduce fluid force and suppress the vortex shedding. Initially, the code's validity was checked, and the effect of the computational domain was studied to determine accurate upstream (L_up), and downstream (L_down) distances and height of channel (H). Subsequently, all the numerical computations were performed by considering the range of Reynolds numbers (Re = U_∞d/ʮ) Re = 80 to 200. The results are presented in terms of vorticity contour, drag (Cd) and lift coefficients (Cl), and physical parameters, including Cd_mean, Cd_rms, Cl_rms, and St. In the vorticity contour, three distinct modes of flow structures were observed for the first configuration (where the control object is placed at the bottom corner of the main object), such as i) Von Karman vortex street (VKVS) flow mode, ii) Two rows vortex street (TRVS) flow mode and iii) Critical flow mode (CF). For the second configuration, two different types of flow modes are identified, dominating the critical flow behavior, those are i) Irregular vortex shedding (IVS) flow mode and ii) Critical flow (CF) mode. The values of Cd_mean, Cd_rms, Cl_rms, and St are calculated against the Reynolds number. For the main object in both configurations, the value of Cd_mean decreases at the lower range of Reynolds numbers and then continuously increases at larger values of Reynolds numbers. However, for the control object, the mean drag coefficient consistently increased with an increment in the range of Reynolds numbers. The maximum value of Cd_mean is attained at Re = 200, reaching the value of 2.0708 for the configuration where the control object is placed at the top right corner. Similarly, the highest value of the Strouhal number is obtained for the control object; placed at the bottom right corner for C2, with a value of 0.1321 occurring at either Re = 100 or Re = 120.

References

M. M. Zdravkovich, “The effect of interference between circular objects in cross flow,” Strut, J. Fluids, vol. 1, pp. 239–261, 1987.

K. Lam and W. C. Cheung, “Phenomena of vortex shedding and flow interference of three cylinders in different equilateral arrangements,” J. Fluid Mech., vol. 196, pp. 1–26, Nov. 1988, doi: 10.1017/S0022112088002587.

D. Sumner, S. J. Price, and M. P. Païdoussis, “Flow-pattern identification for two staggered circular cylinders in cross-flow,” J. Fluid Mech., vol. 411, pp. 263–303, May 2000, doi: 10.1017/S0022112099008137.

S. Balachandar and S. J. Parker, “Onset of vortex shedding in an inline and staggered array of rectangular cylinders,” Phys. Fluids, vol. 14, no. 10, pp. 3714–3732, Oct. 2002, doi: 10.1063/1.1508101.

M. H. Akbari and S. J. Price, “Numerical investigation of flow patterns for staggered cylinder pairs in cross-flow,” J. Fluids Struct., vol. 20, no. 4, pp. 533–554, May 2005, doi: 10.1016/J.JFLUIDSTRUCTS.2005.02.005.

O. Inoue, W. Iwakami, and N. Hatakeyama, “Aeolian tones radiated from flow past two square cylinders in a side-by-side arrangement,” Phys. Fluids, vol. 18, no. 4, Apr. 2006, doi: 10.1063/1.2191847/915406.

A. Agrawal, L. Djenidi, and R. A. Antonia, “Investigation of flow around a pair of side-by-side square cylinders using the lattice Boltzmann method,” Comput. Fluids, vol. 35, no. 10, pp. 1093–1107, Dec. 2006, doi: 10.1016/J.COMPFLUID.2005.05.008.

J. Niu and Z. Zhu, “Numerical study of three-dimensional flows around two identical square cylinders in staggered arrangements,” Phys. Fluids, vol. 18, no. 4, Apr. 2006, doi: 10.1063/1.2194077/915470.

B. S. Carmo and J. R. Meneghini, “Numerical investigation of the flow around two circular cylinders in tandem,” J. Fluids Struct., vol. 22, no. 6–7, pp. 979–988, Aug. 2006, doi: 10.1016/J.JFLUIDSTRUCTS.2006.04.016.

K. Lee and K. S. Yang, “Flow patterns past two circular cylinders in proximity,” Comput. Fluids, vol. 38, no. 4, pp. 778–788, Apr. 2009, doi: 10.1016/J.COMPFLUID.2008.07.005.

K. Fallah, A. Fardad, N. Sedaghatizadeh, E. Fattahi, and A. Ghaderi, “Numerical Simulation of Flow Around Two Rotating Circular Cylinders in Staggered Arrangement by Multi-Relaxation-Time Lattice Boltzmann Method at Low Reynolds Number,” 2011.

J. K. Ostanek and K. A. Thole, “Wake development in staggered short cylinder arrays within a channel,” Exp. Fluids, vol. 53, no. 3, pp. 673–697, Sep. 2012, doi: 10.1007/S00348-012-1313-5/METRICS.

R. Farzad, M., Amir, B. K., Ehsan, G & Mohammad, “Experimental Measurement of Turbulence Intensity of Flow Over Two object and Circular Object in Tandem Arrangement,” 14th Eur. Turbul. Conf. Lyon, Fr., 2013.

P. Anagnostopoulos and S. A. Seitanis, “Numerical study of aperiodic phenomena past two staggered rows of cylinders in cross-flow,” Ocean Eng., vol. 92, pp. 212–233, Dec. 2014, doi: 10.1016/J.OCEANENG.2014.09.049.

F. Tong, L. Cheng, and M. Zhao, “Numerical simulations of steady flow past two cylinders in staggered arrangements,” J. Fluid Mech., vol. 765, pp. 114–149, Feb. 2015, doi: 10.1017/JFM.2014.708.

D. Chatterjee and S. K. Gupta, “Convective Transport Around Rows of Square Cylinders Arranged in a Staggered Fashion at Moderate Reynolds Number,” Numer. Heat Transf. Part A Appl., vol. 68, no. 4, pp. 388–410, Aug. 2015, doi: 10.1080/10407782.2014.986004.

M. M. Alam, H. Bai, and Y. Zhou, “The wake of two staggered square cylinders,” J. Fluid Mech., vol. 801, pp. 475–507, Aug. 2016, doi: 10.1017/JFM.2016.303.

S. Yang, W. Yan, J. Wu, C. Tu, and D. Luo, “Numerical investigation of vortex suppression regions for three staggered circular cylinders,” Eur. J. Mech. - B/Fluids, vol. 55, pp. 207–214, Jan. 2016, doi: 10.1016/J.EUROMECHFLU.2015.10.004.

J. Aboueian and A. Sohankar, “Identification of flow regimes around two staggered square cylinders by a numerical study,” Theor. Comput. Fluid Dyn., vol. 31, no. 3, pp. 295–315, Jun. 2017, doi: 10.1007/S00162-017-0424-2/METRICS.

M. K. Chauhan, S. Dutta, B. S. More, and B. K. Gandhi, “Experimental investigation of flow over a square cylinder with an attached splitter plate at intermediate reynolds number,” J. Fluids Struct., vol. 76, pp. 319–335, Jan. 2018, doi: 10.1016/J.JFLUIDSTRUCTS.2017.10.012.

S. Fezai, F. Oueslati, and B. Ben-Beya, “Identification of flow states around three staggered square cylinders at two symmetrical arrangements by a numerical investigation,” https://doi.org/10.1142/S012918312050151X, vol. 31, no. 11, Sep. 2020, doi: 10.1142/S012918312050151X.

M. Raheela et al., “Numerical investigations for flow past two square rods in staggered arrangement through Lattice Boltzmann method,” Ann. Math. Phys., pp. 016–027, Jul. 2021, doi: 10.17352/AMP.000021.

M. Cheng, D. S. Whyte, and J. Lou, “Numerical simulation of flow around a square cylinder in uniform-shear flow,” J. Fluids Struct., vol. 23, no. 2, pp. 207–226, Feb. 2007, doi: 10.1016/J.JFLUIDSTRUCTS.2006.08.011.

D. T. Sukop, M. C. & Thorne, “Lattice Boltzmann modeling: an introduction for scientists and Engineers,” Springer Berlin Heidelb., 2005.

D. Yu, R. Mei, L. S. Luo, and W. Shyy, “Viscous flow computations with the method of lattice Boltzmann equation,” Prog. Aerosp. Sci., vol. 39, no. 5, pp. 329–367, Jul. 2003, doi: 10.1016/S0376-0421(03)00003-4.

A. A. Mohammad, “Lattice Boltzmann Method: Fundamentals and Engineering Applications with Computer Codes,” Springer, 2011.

D. A. Wolf-Gladrow, “Lattice-gas cellular automata,” pp. 39–138, 2000, doi: 10.1007/978-3-540-46586-7_3.

S. Chen and G. D. Doolen, “Lattice boltzmann method for fluid flows,” Annu. Rev. Fluid Mech., vol. 30, no. Volume 30, 1998, pp. 329–364, Jan. 1998, doi: 10.1146/ANNUREV.FLUID.30.1.329/CITE/REFWORKS.

“Lattice Boltzmann Method: Fundamentals and Engineering Applications with Computer Codes | SpringerLink.” Accessed: Apr. 19, 2024. [Online]. Available: https://link.springer.com/book/10.1007/978-0-85729-455-5

“Low‐Reynolds‐number flow around a square cylinder at incidence: study of blockage, onset of vortex shedding and outlet boundary condition - Sohankar - 1998 - International Journal for Numerical Methods in Fluids - Wiley Online Library.” Accessed: Apr. 19, 2024. [Online]. Available: https://onlinelibrary.wiley.com/doi/abs/10.1002/%28SICI%291097-0363%2819980115%2926%3A1%3C39%3A%3AAID-FLD623%3E3.0.CO%3B2-P

“CFD ANALYSIS OF 2D UNSTEADY FLOW AROUND A SQUARE CYLINDER.” Accessed: Apr. 19, 2024. [Online]. Available: https://www.researchgate.net/publication/331563254_CFD_ANALYSIS_OF_2D_UNSTEADY_FLOW_AROUND_A_SQUARE_CYLINDER

G. R. Vamsee, M. L. De Tena, and S. Tiwari, “Effect of arrangement of inline splitter plate on flow past square cylinder,” Prog. Comput. Fluid Dyn., vol. 14, no. 5, pp. 277–294, 2014, doi: 10.1504/PCFD.2014.064554.

“Large eddy simulation of the subcritical flow past a circular cylinder: numerical and modeling aspects - Breuer - 1998 - International Journal for Numerical Methods in Fluids - Wiley Online Library.” Accessed: Apr. 19, 2024. [Online]. Available: https://onlinelibrary.wiley.com/doi/abs/10.1002/%28SICI%291097-0363%2819981215%2928%3A9%3C1281%3A%3AAID-FLD759%3E3.0.CO%3B2-%23

A. Okajima, “Strouhal numbers of rectangular cylinders,” J. Fluid Mech., vol. 123, pp. 379–398, 1982, doi: 10.1017/S0022112082003115.